Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)
gợi ý: a)chia 2 vế cho căn 5
đặt \(\frac{1}{\sqrt{5}}=cosa\Rightarrow\frac{2}{\sqrt{5}}=sina\)
khi đó pt <=>sin(x-a)=\(\frac{3}{\sqrt{5}}>1\)
->vô nghiệm
bn giải thích cho mk chỗ này được ko : \(\frac{1}{\sqrt{5}}=\cos a\Rightarrow\frac{2}{\sqrt{5}}=\sin a\)
Đáp án B
Phương trình đã cho tương đương với
Ta biết rằng hàm số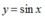
đồng biến trên khoảng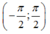 
Ta chỉ ra rằng các hàm số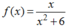
và
Thật vậy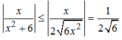
Mặt khác
Từ những đánh giá trên, (5) xảy ra khi và chỉ khi
Tổng các nghiệm của phương trình đã cho là 2 + 6 + 40 = 48.