Vẽ hình liên tiếp theo các cách diễn đạt sau :
a) Vẽ đoạn thẳng AB = 2cm. Vẽ đường tròn (\(C_1\)) tâm A, bán kính AB
b) Vẽ đường tròn \(\left(C_2\right)\) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn \(\left(C_1\right)\) là C và G
c) Vẽ đường tròn \(\left(C_3\right)\) tâm C, bán kính AC. Gọi các giao điểm mới của đường tròn này với đường...
Đọc tiếp
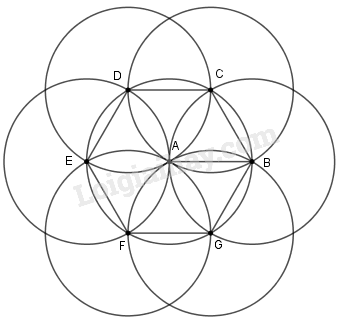
Vẽ hình liên tiếp theo các cách diễn đạt sau :
a) Vẽ đoạn thẳng AB = 2cm. Vẽ đường tròn (\(C_1\)) tâm A, bán kính AB
b) Vẽ đường tròn \(\left(C_2\right)\) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn \(\left(C_1\right)\) là C và G
c) Vẽ đường tròn \(\left(C_3\right)\) tâm C, bán kính AC. Gọi các giao điểm mới của đường tròn này với đường tròn \(\left(C_1\right)\) là D
d) Vẽ đường tròn \(\left(C_4\right)\) tâm D, bán kính AD. Gọi các giao điểm mới của đường tròn này với đường tròn \(\left(C_1\right)\) là E
e) Vẽ đường tròn \(\left(C_5\right)\) tâm E, bán kính AE. Gọi các giao điểm mới của đường tròn này với đường tròn \(\left(C_1\right)\) là F
f) Vẽ đường tròn \(\left(C_6\right)\) tâm F, bán kính AF.
g) Vẽ đường tròn \(\left(C_7\right)\) tâm G, bán kính AG
Sau khi vẽ như trên, hãy so sánh các đoạn thẳng AB, BC, CD, DE, EF, FG, GB

đỉnh F: góc F; \(\widehat{F}\)
đỉnh A: góc BAO; \(\widehat{BAO}\)
đỉnh B: góc B; \(\widehat{B}\)
đỉnh O: góc FOK; góc AOx; góc AOK; góc FOx
\(\widehat{FOK};\widehat{xOA};\widehat{AOK};\widehat{xOF}\)
đỉnh C: góc C; \(\widehat{C}\)
đỉnh F: góc F; \(\widehat{F}\)