
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

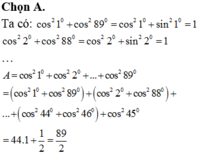

a) Do A + B + C = 180 độ nên góc A bù với góc B + C => sin(B + C) = sinA (sin hai góc bù bằng nhau)
(A + B)/2 + C/2 = 90 độ => hai góc (A + B)/2 và C/2 là hai góc phụ nhau => cos (A + B)/2 = sin(C/2) (Chắc đề bài bạn cho nhầm thành sinC)
b) Bạn xem lại đề nhé
c) \(sin^6a+cos^6a+3sin^2a.cos^2a=\left(sin^2a\right)^3+\left(cos^2a\right)^3+3.sin^2a.cos^2a\)
= \(\left(sin^2a+cos^2a\right)\left(sin^4a+cos^4a-sin^2a.cos^2a\right)+3sin^2a.cos^2a\)
= \(sin^4a+cos^4a+2sin^2a.cos^2a\)
= \(\left(sin^2a+cos^2a\right)^2=1\)

b,(*)chứng minh a=-3b:
xét a-b=2(a+b)
=>a-b=2a+2b
=>-b-2b=2a-a
=>-3b=a (đpcm)
(*) tính a/b :
Từ -3b=a=>a/b=-3
(*)tính a và b:
Ta có : a-b=a/b=-3
và 2(a+b)=a/b=-3
hệ pt<=>a-b=-3
và 2(a+b)=-3
<=>a-b=-3 (1)
và a+b=-1,5 (2)
Lấy (1)+(2),vế theo vế ta đc:
(a-b)+(a+b)=-3+(-1,5)
=>a-b+a+b=-4,5
=>2a=-4,5=>a=-2,25
Mà a-b=-3=>b=0,75
Vậy (a;b)=(-2,25;0,75)
c) vì (x-y2+z)2 >= 0 với mọi x;y;z
(y-2)2 >= 0 với mọi y
(z+3)2 >= 0 với mọi z
=>(x-y2+z)2+(y-2)2+(z+3)2 >= 0 với mọi x;y;z
Mà theo đề: (x-y2+z)2+(y-2)2+(z+3)2=0
=>(x-y2+z)2=(y-2)2=(z+3)2=0
+)(y-2)2=0=>y=2
+)(z+3)2=0=>z=-3
Thay y=2;z=-3 vào (x-y2+z)2=0=>x-22+(-3)2=0=>x=-5
Vậy (x;y;z)=(-5;2;-3)

a) \(4x-7>0\Leftrightarrow4x>7\)\(\Leftrightarrow x>\frac{7}{4}\)
b) \(-5x+8>0\Leftrightarrow5x<8\Leftrightarrow x<\frac{8}{5}\)
c)\(9x-10\le0\Leftrightarrow9x\le10\)\(\Leftrightarrow x\le\frac{10}{9}\)
d) \(\left(x+1\right)^2+4\le x^2+3x+10\)\(\Leftrightarrow x^2-2x+1+4\le x^2+3x+10\)
\(\Leftrightarrow5x\ge-5\Leftrightarrow x\ge-1\)
a,
4x - 7 > 0
↔ 4x > 7
↔ x > \(\dfrac{7}{4}\)
Vậy tập nghiệm của bất phương trình là S = { x / x>\(\dfrac{7}{4}\) }
b,
-5x + 8 > 0
↔ 8 > 5x
↔ \(\dfrac{8}{5}\) > x
Vậy tập nghiệm của bất phương trình là S = { x / \(\dfrac{8}{5}\) > x }
c,
9x - 10 ≤ 0
↔ 9x ≤ 10
↔ x ≤ \(\dfrac{10}{9}\)
Vậy tập nghiệm của bất phương trình là S = { x / x ≤ \(\dfrac{10}{9}\) }
d,
( x - 1 )\(^2\) + 4 ≤ x\(^2\) + 3x + 10
↔ x\(^2\) - 2x +1 +4 ≤ x\(^2\) + 3x + 10
↔ 1 + 4 - 10 ≤ x \(^2\) - x\(^2\) + 3x + 2x
↔ -5 ≤ 5x
↔ -1 ≤ x
Vậy tập nghiệm của bất phương trình là S = { x / -1 ≤ x}

Câu 1.
a). 2A = 8 + 2 3 + 2 4 + . . . + 2 21.
=> 2A – A = 2 21 +8 – ( 4 + 2 2 ) + (2 3 – 2 3) +. . . + (2 20 – 2 20). = 2 21.
b). (x + 1) + ( x + 2 ) + . . . . . . . . + (x + 100) = 5750
=> x + 1 + x + 2 + x + 3 + . . . . . . .. . .. . . . + x + 100 = 5750
=> ( 1 + 2 + 3 + . . . + 100) + ( x + x + x . . . . . . . + x ) = 5750
=> 101 . 50 + 100 x = 5750
100 x + 5050 = 5750
100 x = 5750 – 5050
100 x = 700
x = 7
101 . 50 + 100 x = 5750
100 x + 5050 = 5750
100 x = 5750 – 5050
100 x = 700
x = 7
Câu 1. a). 2A = 8 + 2 3 + 2 4 + . . . + 2 21.
=> 2A – A = 2 21 +8 – ( 4 + 2 2 ) + (2 3 – 2 3) +. . . + (2 20 – 2 20). = 2 21.
b). (x + 1) + ( x + 2 ) + . . . . . . . . + (x + 100) = 5750
=> x + 1 + x + 2 + x + 3 + . . . . . . .. . .. . . . + x + 100 = 5750
=> ( 1 + 2 + 3 + . . . + 100) + ( x + x + x . . . . . . . + x ) = 5750
=> 101 . 50 + 100 x = 5750
100 x + 5050 = 5750
100 x = 5750 – 5050
100 x = 700
x = 7

a: \(\Leftrightarrow A=-\left(x^2-xy^2+2xz-3y^2\right)=-x^2+xy^2-2xz+3y^2\)
b: Vì tổng của B với \(4x^2y+5y^2-xz+z^2\) là một đa thức không chứa biến x nên \(B=-4x^2y+xz\)

1) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/16

Trong đây có câu giống hệt: print - Thư viện Đề thi & Kiểm tra
Ở bài 17 í

Ta có: a +b +c = 0:
=> (a + b + c)2 = 0
=> a² + b² + c² + 2(ab + bc + ca) = 0
=> a² + b² + c² = -2(ab + bc + ca) (1)
Mặt khác:
a^4 + b^4 + c^4 = 2(a²b² + b²c² + c²a²)
=> (a² + b² + c²)² = 4(a²b² + b²c² + c²a²) (cộng 2 vế cho 2(a²b² + b²c² + c²a²) )
=> [-2(ab + bc + ca)]2 = 4(a²b² + b²c² + c²a²) ( do (1) )
<=> 4.(a²b² + b²c² + c²a²) + 8.(ab²c + bc²a + a²bc) = 4(a²b² + b²c² + c²a²)
<=> 8.(ab²c + bc²a + a²bc) = 0
<=> 8abc.(a + b + c) = 0
<=> 0 = 0 (đúng), Vì a + b + c = 0
=> ĐPCM.![]()
xl, mik mới chứng minh đc bằng và cũng có sai sót trong bài làm![]()