Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi z= a + bi \(\left(a,b\in R\right)\)
(2+i)(a+bi)=4-3i
\(\Leftrightarrow\) \(2a-b+\left(a+2b\right)i=4-3i\)
\(\Leftrightarrow\begin{cases}2a-b=4\\a+2b=-3\end{cases}\)
\(\Leftrightarrow\begin{cases}a=1\\b=-2\end{cases}\)
\(z=1-2i\)
w= i(1-2i) + 2( 1+ 2i) = 4 + 5i

Gọi \(z=a+bi\left(a,b\in R\right)\)
\(\left(2+i\right)\left(a+bi=4-3i\right)\)
\(\Leftrightarrow2a-b+\left(a+2b\right)i=4-3i\)
\(\Leftrightarrow\begin{cases}2a-b=4\\a+2b=-3\end{cases}\)
\(\Leftrightarrow\begin{cases}a=1\\b=-2\end{cases}\)
\(z=1-2i\)
\(w=i\left(1-2i\right)+2\left(1+2i\right)=4+5i\)

đặc : \(z=a+bi\) với \(a;b\in R\) và \(i^2=-1\)
ta có : \(\left|z\right|-2\left|\overline{z}\right|=-7+3i+z\Leftrightarrow\left|z\right|-2\left|\overline{z}\right|=\left(a-7\right)+\left(b+3\right)i\)
\(\Leftrightarrow-\sqrt{a^2+b^2}=\left(a-7\right)+\left(b+3\right)i\)
\(\Leftrightarrow\left[{}\begin{matrix}b+3=0\\a-7=-\sqrt{a^2+b^2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}b=-3\\a-7=-\sqrt{a^2+9}\end{matrix}\right.\)
\(\Rightarrow\left(a-7\right)^2=a^2+9\Leftrightarrow a^2-14a+49=a^2+9\Leftrightarrow a=\dfrac{20}{7}\)
\(\Rightarrow z=\dfrac{20}{7}-3i\)
\(\Rightarrow w=1-z+z^2=1-\dfrac{20}{7}+3i+\left(\dfrac{20}{7}-3i\right)^2\)
\(=1-\dfrac{20}{7}+3i+\dfrac{400}{49}-\dfrac{120}{7}i-9=\dfrac{-132}{49}-\dfrac{99}{7}i\)
\(\Rightarrow\left|w\right|=\sqrt{\left(\dfrac{-132}{49}\right)^2+\left(\dfrac{-99}{7}\right)^2}=???\)
khác tất cả các đáp án \(\Rightarrow\) ai xem thử có sai chổ nào không chỉ với .
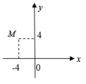
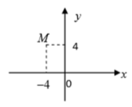
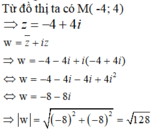
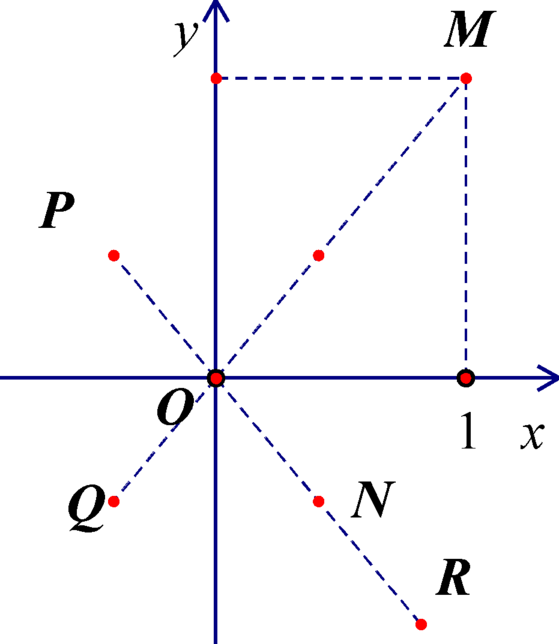




Đáp án D