
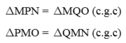
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

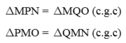

Tam giác DKE có:
+
+
=900 (tổng ba góc trong của tam giác).
+800 +400=1800
=1800 -1200=
Nên
∆ ABC và ∆KDE có:
AB=KD(gt)
=
=600và BE= ED(gt)
Do đó ∆ABC= ∆KDE(c.g.c)
Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại .
hay ∠D + +800 +400 = 1800
⇒∠D = 1800 -1200 = 600
Xét ∆ ABC và ∆KDE có:
AB = KD(gt)
∠B = ∠D ( cùng = 600 )
và BE = ED (gt)
Do đó ∆ABC= ∆KDE (c.g.c)

∆ABC và ∆ABD có:
∠CAB = ∠DAB(gt)
AB là cạnh chung.
∠CBA = ∠DBA (gt)
Nên ∆ABC=∆ABD(g.c.g)
Ta có:
∠ABC + ∠ABD =1800 (Hai góc kề bù).
∠ACB + ∠ACE =1800
Mà ∠ABC = ∠ACB(gt)
Nên ∠ABD = ∠ACE
* ∆ABD và ∆ACE có:
∠ABD = ∠ACE (cmt)
BD=EC(gt)
∠ADB = ∠AEC (gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
∠ADC = ∠AEB (gt)
∠ACD = ∠ABE (gt)
Ta có: DC = DB + BC
EB = EC + BC
Mà BD = EC (gt)
⇒ DC = EB
Nên ∆ADC=∆AEB(g.c.g)

\(\widehat{A}\)=600, \(\widehat{H}\)=700, \(\widehat{E}\)=400
\(\widehat{L}\)=700, \(\widehat{RNQ}\)=800, \(\widehat{NRP}\)=800

Hình 68.
Xét \(\Delta ABC;\Delta ABD\):
AC = AD (gt)
AB chung
BC = BD (gt)
=> \(\Delta ABC=\Delta ABD\left(c.c.c\right)\)
Hình 69.
Xét \(\Delta MNQ;\Delta QPM:\)
MN = QP (gt)
MQ chung
NQ = PM (gt)
=> \(\Delta MNQ=\Delta QPM\left(c.c.c\right)\)
Hình 70. Gọi giao điểm của HK và EI là O.
Xét tg HEI; tg KIE:
EH = KI
EI chung
HI = KE
=> tg HEI = tg KIE (c.c.c)
=> g HEI = g KIE hay g HEO = g OIK
Tương tự: tg HIK = tg KEH (c.c.c)
=> g IHK = g EKH hay g IHO = g OKE
Xét tg HEO; tg KIO:
g HEO = g OIK (c/m trên)
HE = KI
g EHO = g OKI (cộng góc)
=> tg HEO = tg KIO (g.c.g)
Tương tự: tg HIO = tg KEO (g.c.g)

Giải:
Hình 82.
∆ADB và ∆ADE có:
AB=AE(gt)
\(\widehat{A_1}=\widehat{A_2}\)
AD chung.
Nên ∆ADB = ∆ADE(c.g.c)
Hình 83.
∆HGK và ∆IKG có:
HG=IK (gt)
\(\widehat{G}=\widehat{K}\) (gt)
GK là cạnh chung(gt)
Nên ∆HGK = ∆IKG( c.g.c)
Hình 84.
∆PMQ và ∆PMN có:
MP cạnh chung
\(\widehat{M_1}=\widehat{M_2}\)
Nhưng MN không bằng MQ. Nên \(\Delta\)PMQ không bằng \(\Delta\)PMN.
- Hình 82
Xét ΔADB và ΔADE có:
AB = AE (gt)
AD cạnh chung
Nên ΔADB = ΔADE (c.g.c)
Vậy ΔADB = ΔADE- Hình 83
Xét ΔHGK và ΔIKG có:
HG = IK (gt)
GK cạnh chung
Nên ΔHGK = ΔIKG
Vậy ΔHGK = ΔIKG
- Hình 84
Xét ΔPMQ và ΔPMN có:
PM cạnh chung
Nhưng MN không bằng MQ
Nên ΔPMQ không bằng ΔPMN
Vậy ΔPMQ không bằng ΔPMN

Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được.
Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được.