Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ Các đáp án B, C, D chỉ đúng khi các điểm này nằm trên cùng một phương truyền sóng.
\(\rightarrow\) Chọn đáp án A
2/ Khi các sóng truyền từ không khí vào nước thì tần số sóng không đổi còn bước sóng thay đổi sao cho \(f=\frac{v}{\lambda}=\)const .Khi truyền từ không khí vào nước vận tốc của sóng âm tăng nên bước sóng sẽ tăng, vận tốc của sóng ánh sáng giảm nên bước sóng sẽ giảm.
\(\rightarrow\)Chọn đáp án B

Đáp án B.
Khi cho lần lượt C = C 0 = 40 pF, C = C 1 = 10 pF và C = C 2 = 640 pF thì thu được sóng điện từ có bước sóng tương ứng là:
λ 0 = v f 0 = v 1 2 π LC 0 = v . 2 π . LC 0 λ 1 = v f 1 = v 1 2 π LC 1 = v . 2 π . LC 1 λ 2 = v f 2 = v 1 2 π LC 2 = v . 2 π . LC 2
Với v là vận tốc truyền sóng điện từ. Từ đó ta thấy:
λ 1 λ 0 = c 1 c 0 ; λ 2 λ 0 = c 2 c 0 ⇒ λ 1 = λ 0 c 1 c 0 = 20 . 10 40 = 10 ( m ) λ 2 = λ 0 c 2 c 0 = 20 . 640 40 = 80 ( m )

Đáp án B
Khi cho lần lượt C = C 0 = 40 p F , C = C 1 = 10 p F và C = C 2 = 640 p F thì thu được sóng điện từ có bước sóng tương ứng là:
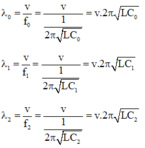
Với v là vận tốc truyền sóng điện từ. Từ đó ta thấy:
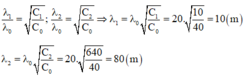

Mình hướng dẫn thế này rồi bạn làm tiếp nhé.
a. Áp dụng CT: \(hf=A_t+\dfrac{1}{2}mv^2\)
\(\Rightarrow 6,625.10^{-34}.3.10^8=A_t+\dfrac{1}{2}.9,1.10^{-31}.(0,4.10^6)^2\)
\(\Rightarrow A_t\)
Mà \(A_t=\dfrac{hc}{\lambda_0}\Rightarrow \lambda_0\)
b. Áp dụng: \(\dfrac{hc}{\lambda}=A_t+eV_{max}\)
\(\Rightarrow \lambda\)

Đáp án B
Phương pháp: Bước sóng![]()
Cách giải:
Bước sóng mà máy thu được có giá trị nằm trong khoảng từ
![]()
Ta có:![]()
![]()
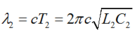
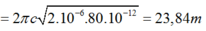
=> Chọn B

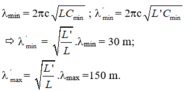

Đáp án B