OLM ưu đãi đặc biệt gói SVIP 18 THÁNG dành cho nhà trường, đăng kí ngay!

OLM tuyển CTV cộng đồng hỏi đáp, đăng kí ngay!

K
Khách

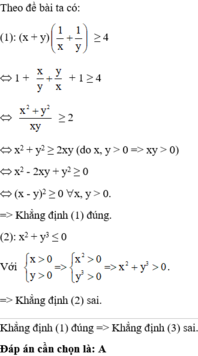
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
L
letomanh
10 tháng 3 2020 - olm

Cho P= \(\frac{x^2+x}{x^2-2x+1}\) : ( \(\frac{x+1}{x}\)- \(\frac{1}{1-x}\)+ \(\frac{2-x^2}{x^2-x}\) )

a)Rút gọn P

b)Tính P với x2 +2x -3 = 0

c)Tìm giá trị nhỏ nhất của P khi x >0
#Hỏi cộng đồng OLM #Toán lớp 8
3
TT
Trí Tiên
10 tháng 3 2020

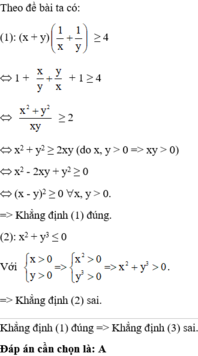
ĐKXĐ : \(x\ne\pm1\)

a) Ta có : 

\(P=\frac{x^2+x}{x^2-2x+1}:\left(\frac{x+1}{x}-\frac{1}{1-x}+\frac{2-x^2}{x^2-x}\right)\)

\(=\frac{x\left(x+1\right)}{\left(x-1\right)^2}:\left(\frac{\left(x-1\right)\left(x+1\right)+x+2-x^2}{x\left(x-1\right)}\right)\)

\(=\frac{x\left(x+1\right)}{\left(x-1\right)^2}:\left(\frac{x+1}{x\left(x-1\right)}\right)\)

\(=\frac{x\left(x+1\right)}{\left(x-1\right)^2}\cdot\frac{x\left(x-1\right)}{x+1}=\frac{x^2}{x-1}\)

Vậy : \(P=\frac{x^2}{x-1}\)

b) Ta có : \(x^2+2x-3=0\)

\(\Leftrightarrow x^2+3x-x-3=0\)

\(\Leftrightarrow\left(x+3\right)\left(x-1\right)=0\)

\(\Leftrightarrow x=-3\) ( Do \(x=1\) không thỏa mãn ĐKXĐ )

Thay \(x=-3\) vào P ta có :

\(P=\frac{\left(-3\right)^2}{-3-1}=\frac{9}{-4}=-\frac{9}{4}\)

Vậy : \(P=-\frac{9}{4}\) với x thỏa mãn đề

c)  Phải là : \(x>1\) nhé bạn :

Ta có :

\(P=\frac{x^2}{x-1}=\frac{x^2-1+1}{\left(x-1\right)}=\frac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)}+\frac{1}{x-1}=x+1+\frac{1}{x-1}\)

\(=\left(x-1+\frac{1}{x-1}\right)+2\)

Ta có : \(x>1\Rightarrow x-1>0,\frac{1}{x-1}>0\)

Áp dụng BĐT AM-GM cho 2 số dương ta có :

\(x-1+\frac{1}{x-1}\ge2\)

Do đó : \(P\ge2+2=4\)

Dấu "="xảy ra \(\Leftrightarrow\left(x-1\right)^2=1\Leftrightarrow x=2\) ( Do \(x>1\) )

Vậy : GTNN của P là 4 tại \(x=2\)

Đúng(0)
ND
Noobie :Đ~♡๖ۣۜTεαм ๖ۣۜCà ๖ۣۜKhịa >....
10 tháng 3 2020

bài này mình cux ko bt làm

Đúng(0)
MT
Minh Tuấn
2 tháng 4 2020 - olm

Cho 2 biểu thức:

A=\(\frac{x+1}{x-2}\)    và B=\(\frac{x^2}{x^2-4}\)

a. Tìm điều hiện xác định phân thức A

b. Tìm x để A=0

c. Tìm giá trị của phân thức B khi x=\(-\frac{1}{2}\)

d. Thực hiện phép tính A-B
#Hỏi cộng đồng OLM #Toán lớp 8
1
NM
nguyễn mạnh long
2 tháng 4 2020

a, đkxđ:x# 2 ,  x# -2

b, 

     A  =   \(\frac{x+1}{x-2}\)=0

<=>      x + 1 = 0

<=>      x = -1

c,B=\(\frac{x2}{x^2-4}\)

Mà x= \(-\frac{1}{2}\)

<=> \(\frac{1}{4}:\left(\frac{1}{4}-4\right)\)

<=>\(\frac{1}{4}:\frac{-15}{4}\)

<=>\(\frac{1}{4}.\frac{4}{-15}\)

<=>\(\frac{-1}{15}\)

d, \(A-B=\frac{x+1}{x-2}-\frac{x^2}{x^2-4}\)

                \(=\frac{\left(x+1\right)\left(x+2\right)-x^2}{\left(x-2\right)\left(x+2\right)}\)

                \(=\frac{x^2+3x+2-x^2}{\left(x-2\right)\left(x+2\right)}\)

                \(=\frac{3x+2}{\left(x-2\right)\left(x+2\right)}\)

Đúng(0)
#𝒌𝒂𝒎𝒊ㅤ♪
17 tháng 12 2019 - olm
Cho biểu thức \(P=\frac{x^2+2x}{2x+10}+\frac{x-5}{x}+\frac{50-5x}{2x\left(x+5\right)}\)a) Tìm điều kiện của của x để giá trị của phân thức xác định b) Tìm x để P = 0 c) Tìm x để \(P=-\frac{1}{4}\)d) Tìm x để \(P>0;P<...
Đọc tiếp

Cho biểu thức \(P=\frac{x^2+2x}{2x+10}+\frac{x-5}{x}+\frac{50-5x}{2x\left(x+5\right)}\)

a) Tìm điều kiện của của x để giá trị của phân thức xác định 

b) Tìm x để P = 0 

c) Tìm x để \(P=-\frac{1}{4}\)

d) Tìm x để \(P>0;P< 0\)

 
#Hỏi cộng đồng OLM #Toán lớp 8
4
NT
Nguyễn Thùy Trang
17 tháng 12 2019

a) Phân thức xác định được \(\Leftrightarrow\hept{\begin{cases}2x+10\ne0\\x\ne0\\2x\left(x+5\right)\ne0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x\ne0\\x+5\ne0\end{cases}}\)

Vậy...

Đúng(0)
NT
Nguyễn Thùy Trang
17 tháng 12 2019

b) \(P=\frac{x^2+2x}{2x+10}+\frac{x-5}{x}+\frac{50-5x}{2x\left(x+5\right)}\)

=> \(P=\frac{x\left(x^2+2x\right)+2\left(x-5\right)\left(x+5\right)+50-5x}{2x\left(x+5\right)}\)

=> \(P=\frac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}\)

=> \(P=\frac{x^3+4x^2-5x}{2x\left(x+5\right)}=\frac{x\left(x-1\right)\left(x+5\right)}{2x\left(x+5\right)}=\frac{\left(x-1\right)}{2}\)

\(P=0\Leftrightarrow x-1=0\Leftrightarrow x=1\)

Đúng(0)
LT
Lê Trường Lân
28 tháng 5 2020 - olm
1) Cho các số nguyên x, y, z thỏa mãn x, y > 1 và \(\frac{4x-4y}{2xy+z}=z\) Chứng minh rằng z = 02) Tìm các số nguyên x thỏa mãn \(x^4-x^2+2x+2\) là số chính phương.3) Tìm các số nguyên x, y thỏa mãn \(x^4+x^2-y^2+y+10=0\).Ai nhanh và đúng, mình sẽ đánh dấu và thêm bạn bè nhé. Thanks. Làm ơn giúp mình !!!...
Đọc tiếp

1) Cho các số nguyên x, y, z thỏa mãn x, y > 1 và \(\frac{4x-4y}{2xy+z}=z\) Chứng minh rằng z = 0

2) Tìm các số nguyên x thỏa mãn \(x^4-x^2+2x+2\) là số chính phương.

3) Tìm các số nguyên x, y thỏa mãn \(x^4+x^2-y^2+y+10=0\).

Ai nhanh và đúng, mình sẽ đánh dấu và thêm bạn bè nhé. Thanks. Làm ơn giúp mình !!! PLEASE!!!
#Hỏi cộng đồng OLM #Toán lớp 8
1
MN
Minh Nguyen
5 tháng 6 2020

2) \(x^4-x^2+2x+2\)

\(=x^2\left(x-1\right)\left(x+1\right)+2\left(x+1\right)\)

\(=x^2\left(x-1+2\right)\left(x+1\right)\)

\(=x^2\left(x+1\right)^2\)

\(=\left(x^2+x\right)^2\)

Vậy \(x^4-x^2+2x+2\)là số chính phương với mọi số nguyên x

Đúng(0)
LT
Lê Trường Lân
28 tháng 5 2020 - olm
1) Cho các số nguyên x, y, z thỏa mãn x, y > 1 và \(\frac{4x-4y}{2xy+z}=z\) Chứng minh rằng z = 02) Tìm các số nguyên x thỏa mãn \(x^4-x^2+2x+2\) là số chính phương.3) Tìm các số nguyên x, y thỏa mãn \(x^4+x^2-y^2+y+10=0\).Ai nhanh và đúng, mình sẽ đánh dấu và thêm bạn bè nhé. Thanks. Làm ơn giúp mình !!!...
Đọc tiếp

1) Cho các số nguyên x, y, z thỏa mãn x, y > 1 và \(\frac{4x-4y}{2xy+z}=z\) Chứng minh rằng z = 0

2) Tìm các số nguyên x thỏa mãn \(x^4-x^2+2x+2\) là số chính phương.

3) Tìm các số nguyên x, y thỏa mãn \(x^4+x^2-y^2+y+10=0\).

Ai nhanh và đúng, mình sẽ đánh dấu và thêm bạn bè nhé. Thanks. Làm ơn giúp mình !!! PLEASE!!!
#Hỏi cộng đồng OLM #Toán lớp 8
0
H2
Hiếu 2k6
16 tháng 3 2020 - olm
Bài 1: Tìm điều kiện xác định của phương trình: \(a.\frac{5-x}{x^2+6x+9}=\frac{3x+2}{x^2+6x+8}\)\(b.\frac{x-7}{x^2+1}=\frac{x+6}{x^2+x+1}\)Bài 2: Giải phương...
Đọc tiếp

Bài 1: Tìm điều kiện xác định của phương trình:

\(a.\frac{5-x}{x^2+6x+9}=\frac{3x+2}{x^2+6x+8}\)

\(b.\frac{x-7}{x^2+1}=\frac{x+6}{x^2+x+1}\)

Bài 2: Giải phương trình:

\(a.\frac{15x-10}{x^2+3}=0\)

\(b.\frac{x^2-4x-5}{x-5}=0\)

\(c.\frac{3x-1}{x-1}-\frac{2x+5}{x+3}-\frac{8}{x^2+2x-3}=0\)
#Hỏi cộng đồng OLM #Toán lớp 8
0
PX
Phạm Xuân Tùng
3 tháng 4 2020 - olm
BÀI 2:GIẢI CÁC PHƯƠNG TRÌNH...
Đọc tiếp

BÀI 2:GIẢI CÁC PHƯƠNG TRÌNH SAU

a) \(\left(9x^2-4\right)\left(x+1\right)=\left(3x+2\right)\left(x^2-1\right)\)

b) \(\left(x-1\right)^2-1+x^2=\left(1-x\right)\left(x+3\right)\)

c) \(\left(x^2-1\right)\left(x+2\right)\left(x-3\right)=\left(x-1\right)\left(x^2-4\right)\left(x+5\right)\)

d) \(x^4+x^3+x+1=0\)

e)\(x^3-7x+6=0\)

f) \(x^4-4x^3+12x-9=0\)

g) \(x^5-5x^3+4=0\)

h) \(x^4-4x^3+3x^2+4x-4=0\)
#Hỏi cộng đồng OLM #Toán lớp 8
0
K
kkk
16 tháng 3 2020 - olm
Bài 1: Tìm điều kiện xác định của phương trình:\(a.\frac{5-x}{x^2+6x+9}=\frac{3x+2}{x^2+6x+8}\)\(b.\frac{x-7}{x^2+1}=\frac{x+6}{x^2+x+1}\)Bài 2: Giải phương...
Đọc tiếp

Bài 1: Tìm điều kiện xác định của phương trình:

\(a.\frac{5-x}{x^2+6x+9}=\frac{3x+2}{x^2+6x+8}\)

\(b.\frac{x-7}{x^2+1}=\frac{x+6}{x^2+x+1}\)

Bài 2: Giải phương trình:

\(a.\frac{15x-10}{x^2+3}=0\)

\(b.\frac{x^2-4x-5}{x-5}=0\)

\(c.\frac{3x-1}{x-1}-\frac{2x+5}{x+3}-\frac{8}{x^2+2x-3}=0\)
#Hỏi cộng đồng OLM #Toán lớp 8
0
ND
Noobie :Đ~♡๖ۣۜTεαм ๖ۣۜCà ๖ۣۜKhịa >....
13 tháng 3 2020 - olm

Cho biểu thức : A = ( \(\frac{2x}{2x^2-5x+3}\) - \(\frac{5}{2x-3}\) ) : ( 3 + \(\frac{5}{x}\) )

a)Rút gọn A

b)Tính giá trị của x để A = 2

C)Tìm x để A > 0
#Hỏi cộng đồng OLM #Toán lớp 8
10
PL
Phước Lộc
13 tháng 3 2020

bạn ơi bạn kiểm tra lại đề thêm lần nữa xem có sai ko ?

Đúng(0)
PL
Phước Lộc
13 tháng 3 2020

câu a mình rút gọn ra:

\(A=\frac{5-3x}{\left(2x-3\right)\left(x-1\right)}.\frac{x}{5+3x}\)

tới đây hết rút được rồi

Đúng(0)
ND
Noobie :Đ~♡๖ۣۜTεαм ๖ۣۜCà ๖ۣۜKhịa >....
11 tháng 3 2020 - olm

Cho biểu thức : A= (\(\frac{2+x}{2-x}\) - \(\frac{2-x}{2+x}\) - \(\frac{4x^2}{x^2-4}\) ) : \(\frac{x^2-6x+9}{\left(2-x\right)\left(x-3\right)}\)

a)Tìm điều kiện để biến x để A có nghĩa?Rút gọn A.

b)Tìm x để A = 1

c)Tìm x để A > 0?
#Hỏi cộng đồng OLM #Toán lớp 8
3
KN
Kiệt Nguyễn
11 tháng 3 2020

a) A có nghĩa\(\Leftrightarrow\hept{\begin{cases}2-x\ne0\\2+x\ne0\\x-3\ne0\end{cases}}\Rightarrow x\ne\pm2;x\ne3\)

\(A=\left(\frac{2+x}{2-x}-\frac{2-x}{2+x}-\frac{4x^2}{x^2-4}\right):\frac{x^2-6x+9}{\left(2-x\right)\left(x-3\right)}\)

\(=\frac{\left(2+x\right)^2-\left(2-x\right)^2+4x^2}{4-x^2}:\frac{\left(x-3\right)^2}{\left(2-x\right)\left(x-3\right)}\)

\(=\frac{x^2+4x+4-4+4x-x^2+4x^2}{4-x^2}:\frac{x-3}{2-x}\)

\(=\frac{4x^2+8x}{4-x^2}.\frac{2-x}{x-3}\)

\(=\frac{4x\left(x+2\right)}{\left(2+x\right)\left(x-3\right)}=\frac{4x}{x-3}\)

b) \(A=1\Leftrightarrow4x=x-3\Leftrightarrow x=-1\)

c) \(A>0\Leftrightarrow\frac{4x}{x-3}>0\)

TH1: \(\hept{\begin{cases}4x>0\\x-3>0\end{cases}}\Leftrightarrow x>3\)

TH2: \(\hept{\begin{cases}4x< 0\\x-3< 0\end{cases}}\Leftrightarrow x< 0\)

Đúng(0)
ND
Noobie :Đ~♡๖ۣۜTεαм ๖ۣۜCà ๖ۣۜKhịa >....
11 tháng 3 2020

Giúp mình với đúng mik tích cho :>>

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP