Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a\()\)
Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính: 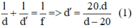
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
L = 125cm
∗ Trường hợp 1: A’B’ là ảnh thật → d’ > 0
→ L = d’ + d =125cm (2)
Từ (1) và (2) ta có:
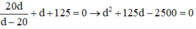
Giải phương trình lấy nghiệm d1 > 0 ta được: d1 = 17,54 cm
∗ Trường hợp 2
d’ + d = - 125cm (trường hợp này thì ảnh A’B’ là ảnh ảo) (3)
Từ (1) và (3) ta có:
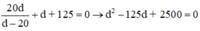
Giải phương trình lấy nghiệm d > 0 ta được: d = 25cm hoặc d = 100cm
a\()\)
Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính: 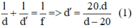
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
L = 125cm
∗ Trường hợp 1: A’B’ là ảnh thật → d’ > 0
→ L = d’ + d =125cm (2)
Từ (1) và (2) ta có:
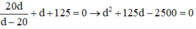
Giải phương trình lấy nghiệm d1 > 0 ta được: d1 = 17,54 cm
∗ Trường hợp 2
d’ + d = - 125cm (trường hợp này thì ảnh A’B’ là ảnh ảo) (3)
Từ (1) và (3) ta có:
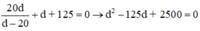
Giải phương trình lấy nghiệm d > 0 ta được: d = 25cm hoặc d = 100cm

Sơ đồ tạo ảnh:

Khoảng cách giữa vật và ảnh qua thấu kính


Vì vật là vật thật nên ta có 3 nghiệm thỏa mãn bài toán:
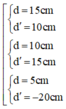


b) Để có 1 vị trí của thấu kính cho ảnh rõ nét trên màn thì phương trình (*) phải có nghiệm kép nên:
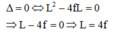
c) Để không có vị trí của thấu kính cho ảnh rõ nét trên màn thì phương trình (*) phải vô nghiệm nên:
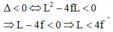

Ta có hệ là ảnh thật
\(\Rightarrow d'>0\\ \Leftrightarrow\left\{{}\begin{matrix}d+d'=45\\\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{10}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d+d'=45\\\dfrac{d+d'}{d.d'}=\dfrac{1}{10}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d+d'=45\\d.d'=450\end{matrix}\right.\)
Áp dụng Vi ét ta có d & d' là no của pt
\(x^2-45x+450=0\Leftrightarrow\left\{{}\begin{matrix}x_1=15\\x_2=30\end{matrix}\right.\)
Ảnh > vật ( d > d' )
\(\Rightarrow d'=30,d=15\)
b, Kcách từ ảnh đến vật là d' + d = s
\(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}\Rightarrow d'=\dfrac{df}{d-f}\Rightarrow s=d+\dfrac{df}{df}\\ s'd=1+\dfrac{f\left(d-f\right)-df}{\left(d-f\right)^2}=1-\dfrac{f^2}{\left(d-f\right)^2}\)
Tại \(d=15\Rightarrow s'd\left(15\right)=-3\)
--> d tăng s giảm
--> ảnh dịch lại gần vật
hệ thức Vi-ét làm gì dợ Châu bà giải delta là ra gòi:v ( mà cái này có Vi-ét à ?? ):))

Chọn đáp án B
Vị trí của ảnh: d / = d f d − f = 10.20 10 − 20 = − 20 c m < 0
→ Ảnh ảo, cùng chiều, cách thấu kính 20cm
Độ phóng đại của ảnh: k = − d / d = 2 ⇒ Ảnh cao gấp hai lần vật

Đáp án: B
HD Giải:
Vật đặt trong tiêu cự nên cho ảnh ảo cùng chiều với vật
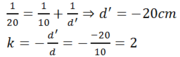
ảnh cao gấp đôi lần vật
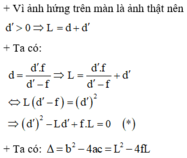

Thấu kính cho ảnh thật A'B' cao gấp \(\frac{1}{3}\) lần vật AB ⇒ k = \(-\frac{1}{3}\) = \(-\frac{d'}{d}\) ⇒ d' = \(\frac{d}{3}\)
mà \(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\) ⇔ \(\frac{1}{15}=\frac{1}{d}+\frac{1}{\frac{d}{3}}\) ⇔ d = 60 (cm) ⇒ d' = 20 (cm)
Vậy vị trí của vật là cách thấu kính 60 cm và vị trí của ảnh là cách thấu kính 20 cm.