Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lần sau em đăng bài ở học 24 để mọi người giúp đỡ em nhé!
Link đây: Cộng đồng học tập online | Học trực tuyến
1. Gọi I là tâm của mặt cầu cần tìm
Vì I thuộc d
=> I( a; -1; -a)
Mặt cầu tiếp xúc với hai mặt phẳng (p), (Q). nên ta co:
d(I; (P))=d(I;(Q))
<=> \(\frac{\left|a+2\left(-1\right)+2\left(-a\right)+3\right|}{\sqrt{1^2+2^2+2^2}}=\frac{\left|a+2\left(-1\right)+2\left(-a\right)+7\right|}{\sqrt{1^2+2^2+2^2}}\)
\(\Leftrightarrow\frac{\left|-a+1\right|}{3}=\frac{\left|-a+5\right|}{3}\Leftrightarrow a=3\)
=> I(3; -1; -3) ; bán kinh : R=d(I; P)=2/3
=> Phương trình mặt cầu:
\(\left(x-3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
đáp án C.
2. Gọi I là tâm mặt cầu: I(1; -1; 0)
Ta có: Phương trình mặt phẳng (P) tiếp xúc vs mặt Cầu S tại M
=> IM vuông góc vs mặt phẳng (P)
=> \(\overrightarrow{n_p}=\overrightarrow{MI}=\left(1;0;0\right)\)
=> Phương trình mặt phẳng (P) có véc tơ pháp tuyến: \(\overrightarrow{n_p}\)và qua điểm M
1(x-0)+0(y+1)+0(z-0) =0<=> x=0
đáp án B
3.
\(f\left(x\right)=\dfrac{1}{256}\left(2x+3\right)^{10}=\dfrac{1}{256} \sum \limits_{k=0} ^{10}C_{k}^{10}(2x)^k.3^{10-k}\)
Để có hệ số x^8 thì k=8 khi đó hệ số của x^8 là:
\(\dfrac{1}{256}C_{8}^{10}.2^8.3^{10-8}=405\)
đáp án D
4.
pt <=> \(\left(2.5\right)^{x^2-3}=10^{-2}.10^{3x-3}\)
\(\Leftrightarrow10^{x^2-3}=10^{3x-5}\)
\(\Leftrightarrow x^2-3=3x-5\Leftrightarrow x^2-3x+5=0\)
=> theo định lí viet tổng các nghiệm bằng 3, tích các nghiệm bằng 5
Đáp án A
a) Gọi \(z_1,z_2\) là các nghiệm của phương trình với \(\left|z_1\right|=1\). Từ \(z_2=\frac{c}{a}.\frac{1}{z_1}\) kéo theo \(\left|z_2\right|=\left|\frac{c}{a}\right|.\frac{1}{\left|z_1\right|}=1\)
vì \(z_1+z_2=-\frac{b}{a},\left|a\right|=\left|b\right|\), ta có \(\left|z_1+z_2\right|^2=1\)
Hệ thức tương đương với
\(\left(z_1+z_2\right)\left(\overline{z_1}+\overline{z_2}\right)=1\) tức là \(\left(z_1+z_2\right)\left(\frac{1}{z_1}+\frac{1}{z_2}\right)=1\)
\(\left(z_1+z_2\right)^2=z_1z_2\)
hay \(\left(-\frac{b}{a}\right)^2=\frac{c}{a}\Rightarrow b^2=ac\)
b) Theo câu a) \(b^2=ac,c^2=ab\). Nhân các hệ thức được \(b^2c^2=a^2bc\Rightarrow a^2=bc\)
Do đó \(a^2+b^2+c^2=ab+bc+ca\)
Hệ tương đương với :
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
Tức là
\(\left(a-b\right)^2+\left(b-c\right)^2+2\left(a-b\right)\left(b-c\right)+\left(c-a\right)^2=2\left(a-b\right)\left(b-c\right)\)
Kéo theo
\(\left(a-c\right)^2=\left(a-b\right)\left(b-c\right)\)
Lấy giá trị tuyệt đối, được \(\beta^2=\gamma\alpha\)
Ở đây \(\alpha=\left|b-c\right|,\beta=\left|c-a\right|,\gamma=\left|a-b\right|\)
Tương tự được :
\(\alpha^2=\beta\gamma,\gamma^2=\alpha\beta,\)
Cộng các hệ thức, được :
\(\alpha^2+\beta^2+\gamma^2=\alpha\beta+\beta\gamma+\gamma\alpha\)
Tức là (\(\left(\alpha-\beta\right)^2+\left(\beta-\gamma\right)^2+\left(\gamma-\beta\right)^2=0\)
Do đó : \(\beta=\alpha=\gamma\)
Ta có:
f(x) = ax2 – 2(a + 1)x + a + 2 = (x – 1)(ax – a- 2) nên phương trình f(x) = 0 luôn có hai nghiệm thực là:
x = 1, x=a+2ax=a+2a
Theo định lí Vi-et, tổng và tích của các nghiệm đó là:
S=2a+2a,P=a+2aS=2a+2a,P=a+2a
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số S=2a+2a=2+2aS=2a+2a=2+2a
- Tập xác định : (-∞, 0)∪ (0, +∞)
- Sự biến thiên: S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞)S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞) nên hàm số nghịch biến trên hai khoảng (-∞, 0) và (0, +∞)
- Cực trị: Hàm số không có cực trị
- Giới hạn tại vô cực và tiệm cận ngang
lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2
Vậy S = 2 là tiệm cận ngang
- Giới hạn vô cực và tiệm cận đứng:
lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞
Vậy a = 0 là tiệm cận đứng.
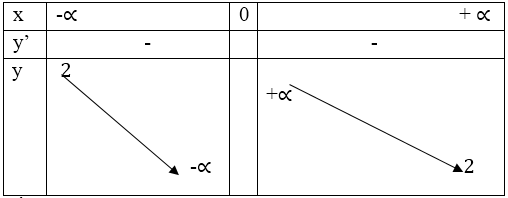
- Bảng biến thiên:
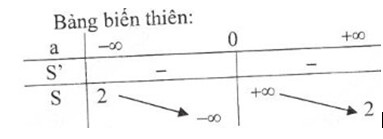
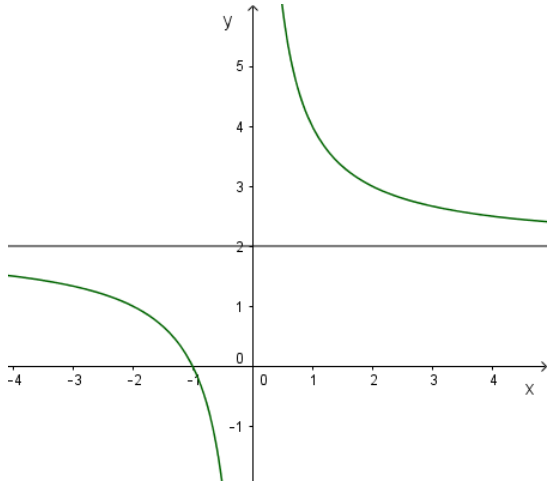
Đồ thị hàm số:
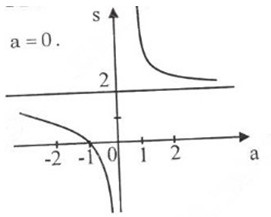
Đồ thị không cắt trục tung, cắt trục hoành tại a = -1
2) Khảo sát sự biến thiên và vẽ đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a
Tập xác định: D = R\{0}
S′=−2a2<0,∀a∈DS′=−2a2<0,∀a∈D
lima→0−S=−∞lima→0−S=−∞⇒ Tiệm cận đứng: a = 0
lima→±∞S=1lima→±∞S=1⇒ Tiệm cận ngang: S = 1
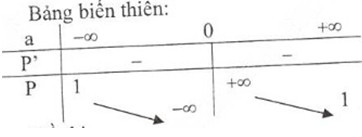
Đồ thị hàm số:
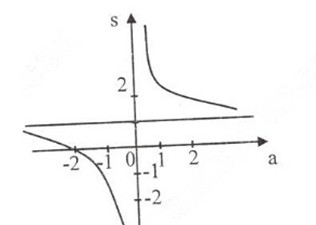
Ngoài ra: đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a có thể nhận được bằng cách tịnh tiến đồ thị S=2a+2a=2+2aS=2a+2a=2+2a dọc theo trục tung xuống phía dưới 1 đơn vị.
Lời giải
khảo sát
TXD mọi x
y' =3x^2 -6x =3x(x-2)
y' =0 => x= 0 hoặc x=2
y'' =6x-6
y''(0) =-6 <0 hàm đạt cực đại tại x=0
y''(2) =6 >0 hàm đạt cực tiểu tại x =2
y'' =0 => x=1 hàm có điểm uốn tại x=1
hàm đi từ - vc--> +vc đi góc (III) lên (IV)
Vẽ đồ thị
Các điểm quan trọng
cực đại A(0,0)
cực tiểu B(2,-4)
uốn C(1,-2)
Các điểm phụ trọng
giao với trục hoành E(0,0); \(F\left(3;0\right)\)
Giao với trục tung: \(A\left(0,0\right)\)
Đồ thị
b)
nhìn vào đồ thị số y=x^3 -3x^2
Hàm số x^3 -3x^2 -m có 3 nghiệm phân biệt
khi 0<m<-4
Gọi \(x_1,x_2\) là các nghiệm phương trình và \(r=\left|x_2\right|=\left|x_2\right|\) Khi đó :
\(\frac{p^2}{q^2}=\frac{\left(x_1+x_2\right)^2}{x_1x_2}=\frac{x_1}{x_2}+\frac{x_2}{x_1}+2=\frac{x_1\overline{x_2}}{r^2}+\frac{x_2\overline{x_1}}{r^2}+2=2+\frac{2}{r^2}Re\left(x_1\overline{x_2}\right)\)
Là số thực, hơn nữa :
\(Re\left(x_1\overline{x_2}\right)\ge-\left|x_1\overline{x_2}\right|=-r^2\)
Do đó \(\frac{p^2}{q^2}\ge0\)
vậy \(\frac{p}{q}\) là một số thực
Chọn A.
+Nếu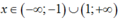
thì x2 – 1 > 0. Suy ra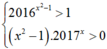 
+ Nếu -1 < x < 1 thì x2 - 1 < 0. Suy ra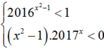
+ Kiểm tra x = 1 ; x = -1 thỏa mãn phương trình đã cho.
Vậy phương trình đã cho có hai nghiệm x = -1 ; x = 1.
Suy ra phương trình đã cho có tổng các nghiệm bằng 0.