


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




+ Vận tốc của electron khi nó chuyển động trên quỹ đạo thứ n: v ~ 1 n
→ Động năng giảm 9 lần → v giảm 3 lần → n = 6.
+ Bước sóng dài nhất ứng với sự chuyển mức năng lượng từ E6 về E5, bước sóng nhìn thấy ngắn nhất ứng với sự chuyển mức năng lượng từ E6 về E2.
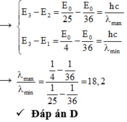

Động lượng của hạt giảm 3 lần --> tốc độ giảm 3 lần --> Vị trí trạng thái tăng 3 lần
Do vậy, e chuyển từ trạng thái 1 lên trạng thái 3.
Bước sóng nhỏ nhất khi nguyên tử chuyển từ mức 3 về mức 1.
\(\Rightarrow \dfrac{hc}{\lambda}=(-\dfrac{1}{3^2}+1).13,6.1,6.10^{-19}\)
\(\Rightarrow \lambda=...\)

Chọn đáp án B
@ Lời giải:
+ Kích thích để nguyên tử chuyển từ trạng thái dừng m lên trạng thái dừng n bằng photon có năng lượng 2,856 eV nên:
E n − E m = 2 , 856 e V ⇒ − 13 , 6 n 2 + 13 , 6 m 2 = 2 , 856 ⇒ − n n 2 + 1 m 2 = 21 100 1
+ Bán kính quỹ đạo tăng lên 6,25 lần nên:
r n r m = n m 2 = 6 , 25 ⇒ n = 2 , 5 m 2
+ Thay (2) vào (1):
− 1 2 , 5 m 2 + 1 m 2 = 21 25 m 2 = 21 100 ⇒ m = 2 n = 2 , 5 m = 5
+ Bước sóng nhỏ nhất mà nguyên tử có thể phát ra sau khi ngừng kích thích ứng với quá trình chuyển mức năng lượng từ quỹ đạo n = 5 về quỹ đạo n = 1:
ε max = E 5 − E 1 = − 13 , 6 25 + 13 , 6 = 13 , 056 e V ⇒ λ min = 1 , 242 13 , 056 = 0 , 0951 μ m = 9 , 51.10 − 8 m

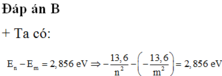
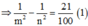

Vậy sau khi bị kích thích, nguyên tử đang tồn tại ở trạng thái dừng O (n=5)
+ Nguyên tử phát ra photon có bước sóng nhỏ nhất khi nó chuyển từ mức năng lượng N (n=5) về K (n=1). Khi đó:
![]()
+ Bước sóng nhỏ nhất mà nguyên tử phát ra:
![]()

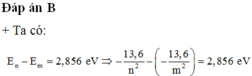
![]()

Vậy sau khi bị kích thích, nguyên tử đang tồn tại ở trạng thái dừng O
+ Nguyên tử phát ra photon có bước sóng nhỏ nhất khi nó chuyển từ mức năng lượng N về K . Khi đó:


Ở trạng thái kích thích thứ nhất: n = 2
Trạng thái kích thích thứ ba: n = 4
Ta có:
\(r_n=r_0.n^2\)
\(\Rightarrow r_2=r_0.4\)
\(r_4=r_0.16\)
\(\Rightarrow \dfrac{r_4}{r_2}=4\Rightarrow r_4=r_2.4=8,48.10^{-10}(m)\)
Chọn A.

Năng lượng của electron ở trạng thái dừng n là \(E_n = -\frac{13,6}{n^2}.(eV)\)
\(hf_1 =\frac{hc}{\lambda_1}= E_3-E_1.(1) \)
\(hf_2 =\frac{hc}{\lambda_2}= E_5-E_2.(2) \)
Chia hai phương trình (1) và (2): \(\frac{\lambda_2}{\lambda_1}= \frac{E_3-E_1}{E_5-E_2}.(3)\)
Mặt khác: \(E_3-E_1 = 13,6.(1-\frac{1}{9}).\)
\(E_5-E_2 = 13,6.(\frac{1}{4}-\frac{1}{25}).\)
Thay vào (3) => \(\frac{\lambda_2}{\lambda_1}= \frac{800}{189}\) hay \(189 \lambda_2 = 800 \lambda_1.\)