Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

bài 1
\(A+B=a+b-5-b-c+1=a-c-4\)
\(A+B+C+D=a-c-4+b-c-4+b-a=2b-2c\)
\(A-B+C-D=a+b-5+b+c-1+b-c-4+a-b\)
\(A-B+C-D=2a+2b-10\)
\(A+B=a-c-4\)
\(C-D=b-c-4-b+a=a-c-4\)
\(A+B=C-D\)

Lời giải:
\(A=a_1a_2+a_2a_3+....+a_{n-1}a_n+a_na_1=0\)
Nếu $n$ lẻ, ta thấy tổng $A$ gồm lẻ số hạng, mỗi số hạng có giá trị $1$ hoặc $-1$ nên $A$ lẻ \(\Rightarrow A\neq 0\) (vô lý)
Do đó $n$ chẵn. Nếu $n$ có dạng $4k+2$. Vì $A=0$ nên trong $4k+2$ số hạng trên sẽ có $2k+1$ số có giá trị là $1$ và $2k+1$ số có giá trị $-1$. Vì mỗi số $a_i$ trong $A$ xuất hiện $2$ lần nên \(a_1a_2a_2a_3....a_{n-1}a_na_{n}a_{1}=(a_1a_2...a_n)^2=1^{2k+1}(-1)^{2k+1}=-1\) (vô lý)
Do đó $n$ phải có dạng $4k$, tức là $n$ chia hết cho $4$ (đpcm)

Đáp án C
Thể tích khối tứ diện OABC là V O A B C = O A . O B . O C 6 = 1
Mà S M N P = 1 4 S A B C → V O . M N P = 1 4 V O . A B C = 1 4

\(\left(a+1\right)+\left(a+2\right)+\left(a+3\right)+\left(a+4\right)+\left(a+5\right)=115\)
\(a+1+a+2+a+3+a+4+a+5=115\)
\(\left(a+a+a+a+a\right)+\left(1+2+3+4+5\right)=115\)
\(5a+15=115\)
\(5a=115-15=100\)
\(a=\frac{100}{5}=20\)
Vậy a=20

a) \(=\frac{3}{17}-\frac{2}{345}+\frac{5}{12}+\frac{2}{345}-\frac{3}{17}+\frac{1}{12}\)
\(=\left(\frac{3}{17}-\frac{3}{17}\right)+\left(\frac{2}{345}-\frac{2}{345}\right)+\left(\frac{5}{12}+\frac{1}{12}\right)\)
\(=\frac{6}{12}=\frac{1}{2}\)
b) \(=-\frac{49}{25}-\frac{5}{36}+\frac{4}{123}+\frac{49}{25}-\frac{4}{123}-\frac{1}{36}\)
\(=\left(-\frac{49}{25}+\frac{49}{25}\right)+\left(\frac{4}{123}-\frac{4}{123}\right)-\left(\frac{5}{36}+\frac{1}{36}\right)\)
\(=-\frac{6}{36}=-\frac{1}{6}\)



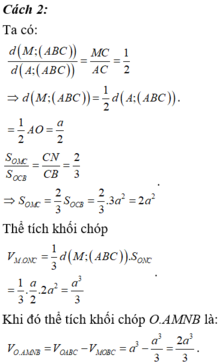
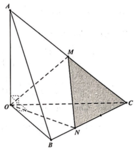

Phương pháp:
Sử dụng công thức tính thể tích khối chóp có chiều cao h và diện tích đáy S là V = 1 3 h . S
Sử dụng công thức tỉ lệ thể tích: Cho hình chóp S.ABCD có M, N, P lần lượt thuộc các cạnh SA, SB, SC.
Cách giải: