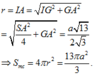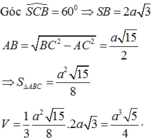Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

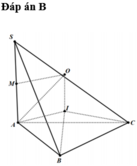
Dựng tam giác đều IAB (I và C cùng phía bờ AB). Ta có ∠ I B C = 120 ° - 60 ° = 60 ° và IB=BC nên DIBC đều, IA=IB=IC=a
Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.
Gọi M là trung điểm của SA.
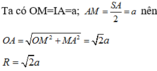

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

Đáp án A
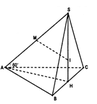
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM // SA. Mà


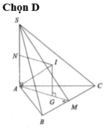
Gọi G là trọng tâm của tam giác đều ABC, suy ra G là tâm đường tròn ngoại tiếp DABC
Trục của đường tròn ngoại tiếp DABC cắt mặt phẳng trung trực của cạnh bên SA tại tâm I của mặt cầu ngoại tiếp hình chóp S.ABC. Tính