
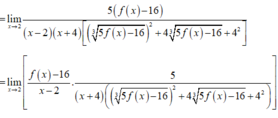

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

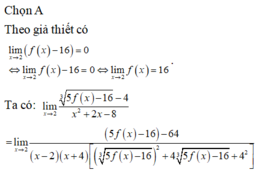
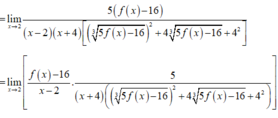


ta có (f(x)-20)/(x-2)=10
===>f(x)=10x
thay f(x)=10x vào A và thay
x=2+0,000000001 ta được giới hạn của A= -331259694,9
cái chỗ F(x) =10x đó ,đâu có là sao vậy ạ , tại có thể 10 đó là g(2)=10

\(a=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x+1\right)\left(x^2+1\right)}{\left(x-1\right)\left(x^2+x-1\right)}=\lim\limits_{x\rightarrow1}\frac{\left(x+1\right)\left(x^2+1\right)}{x^2+x-1}=\frac{4}{1}=4\)
\(b=\lim\limits_{x\rightarrow-1}\frac{\left(x+1\right)\left(x^4-x^3+x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\lim\limits_{x\rightarrow-1}\frac{x^4-x^3+x^2-x+1}{x^2-x+1}=\frac{5}{3}\)
\(c=\lim\limits_{x\rightarrow3}\frac{\left(x+1\right)\left(x-3\right)^2}{\left(x^2+1\right)\left(x^2-9\right)}=\lim\limits_{x\rightarrow3}\frac{\left(x+1\right)\left(x-3\right)}{\left(x^2+1\right)\left(x+3\right)}=\frac{0}{60}=0\)
\(d=\lim\limits_{x\rightarrow1}\frac{4x^6-5x^5+x}{x^2-2x+1}=\lim\limits_{x\rightarrow1}\frac{24x^5-25x^4+1}{2x-2}=\lim\limits_{x\rightarrow1}\frac{120x^4-100x^3}{2}=10\)
\(e=\lim\limits_{x\rightarrow1}\frac{mx^{m-1}}{nx^{n-1}}=\frac{m}{n}\)
\(f=\lim\limits_{x\rightarrow-2}\frac{\left(x+2\right)\left(x-2\right)\left(x^2+4\right)}{\left(x+2\right)x^2}=\lim\limits_{x\rightarrow-2}\frac{\left(x-2\right)\left(x^2+4\right)}{x^2}=-8\)
Hai câu d, e khai triển thì dài quá nên làm biếng sử dụng L'Hopital

Đặt \(\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+....+\frac{1}{n\left(n+1\right)}=A\)
\(\Leftrightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+....+\frac{1}{n}-\frac{1}{n+1}\)
\(\Leftrightarrow A=\frac{n+1}{n+1}-\frac{1}{n+1}=\frac{n}{n+1}\)

Quan sát đồ thị ta thấy x → -∞ thì f(x) → 0; khi x → 3- thì f(x) → -∞;
khi x → -3+ thì f(x) x → +∞.
b) f(x) =
=
= 0.
f(x) =
=
= -∞ vì
=
> 0 và
= -∞.
f(x) =
=
.
= +∞
vì
=
=
> 0 và
= +∞.

a)
=
= -4.
b)
=
=
(2-x) = 4.
c)
=
=
=
=
.
d)
=
= -2.
e)
= 0 vì
(x2 + 1) =
x2( 1 +
) = +∞.
f)
=
= -∞, vì
> 0 với ∀x>0.