


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



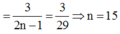

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

Xét tam giác \(PBC\)và tam giác \(PAB\)có:
\(\frac{PB}{PA}=\frac{BC}{AB}=\frac{PC}{PB}=\sqrt{2}\)
suy ra \(\Delta PBC~\Delta PAB\left(c.c.c\right)\)
suy ra \(\widehat{PBC}=\widehat{PAB}\).
\(\widehat{APB}=180^o-\widehat{PAB}-\widehat{PBA}=180^o-\widehat{PBC}-\widehat{PBA}=180^o-\widehat{ABC}\)
\(=180^o-45^o-135^o\)

C K O E H F B A D
Trên \(\Delta\) lấy điểm D sao cho à D, A nằm khác phía nhau so với B. Gọi E là giao điểm của các đường thẳng KA và OC; Gọi F là giao điểm của các đường thẳng KB và OD
Vì K là tâm đường tròn bàng tiếp góc O của tam giác OAB nên KE là phân giác của góc OAC. Mà OAC là tam giác cân tại A ( do OA = AC, theo gt) nên suy ra KE cũng là đường trung trục của OC. Do đó, E là trung điểm của OC và KC=KO
Xét tương tự đối với KF, ta cũng có F là trung điểm của OD và KD=KO
Suy ra tam giác CKD cân tại K. Do đó, hạ KH vuông góc với \(\Delta\) , ta có H là trung điểm của CD. Như vậy :
+ A là giao của \(\Delta\) và đường trung trực \(d_1\) của đoạn OC (1)
+ B là giao của \(\Delta\) và đường trung trực \(d_2\) của đoạn OD, với D là điểm đối xứng của C qua H là hình chiếu vuông góc của K trên \(\Delta\) (2)
Vì \(C\in\Delta\) và có hoành độ \(x_0=\frac{24}{5}\) nên gọi \(y_0\) là tung độ của C, ta có :
\(2.\frac{24}{5}+3y_0-12=0\) suy ra \(y_0=-\frac{12}{5}\)
Từ đó, trung điểm E của OC có tọa độ là \(\left(\frac{12}{5};-\frac{6}{5}\right)\) và đường thẳng OC có phương trình \(x+2y=0\)
Suy ra phương trình của \(d_1\) là \(2x-y-6=0\)
Do đó, theo (1), tọa độ của A là nghiệm của hệ phương trình :
\(\begin{cases}4x+3y-12=0\\2x-y-6=0\end{cases}\)
Giải hệ ta có \(A=\left(3;0\right)\)
Để tìm tọa độ đỉnh B ta làm như sau :
Gọi d là đường thẳng đi qua K(6;6) và vuông góc với \(\Delta\).
Ta có phương trình của d là : \(3x-4y+6=0\). Từ đây, do H là giao điểm của \(\Delta\). và d nên tọa độ của H là nghiệm của hệ phương trình :
\(\begin{cases}4x+3y-12=0\\3x-4y+6=0\end{cases}\)
Giải hệ trên, ta được \(H=\left(\frac{6}{5};\frac{12}{5}\right)\) suy ta \(D=\left(-\frac{12}{5};\frac{26}{5}\right)\)
Do đó, trung điểm F của OD có tọa độ là \(\left(-\frac{6}{5};\frac{18}{5}\right)\) và đường thẳng OD có phương trình \(3x+y=0\)
Suy ra phương trình của \(d_2\) là \(x-3y+12=0\)
Do đó, theo (2), tọa độ B là nghiệm của hệ phương trình :
\(\begin{cases}4x+3y-12=0\\x-3y+12=0\end{cases}\)
Giải hệ trên ta được B=(0;4)

a) Ta có \(\left(C\right):y=\frac{-x+2}{x+1}=-1+\frac{3}{x+1}\)
Dời hệ trục Oxy về hệ trục XIY với công thức dời trục \(\begin{cases}x=X-1\\y=Y-1\end{cases}\)
Ta có phương trình hệ trục tọa độ mới \(Y=\frac{3}{X}\),
Trong hệ trục tọa độ mới, ta giả sử \(M\left(m;\frac{3}{m}\right);N\left(n;\frac{3}{n}\right);P\left(p;\frac{3}{p}\right)\)
Gọi \(H\left(x;y\right)\) là trực tâm của tam giác MNP, ta có : \(\begin{cases}\overrightarrow{MH}.\overrightarrow{NP}=0\\\overrightarrow{NH}.\overrightarrow{MP}=0\end{cases}\) (a)
Mà \(\overrightarrow{MH}=\left(x-m;y-\frac{3}{m}\right);\overrightarrow{NP}=\left(p-n;\frac{3}{p}-\frac{3}{n}\right);\overrightarrow{NH}=\left(x-n;y-\frac{3}{n}\right);\overrightarrow{MP}=\left(p-m;\frac{3}{p}-\frac{3}{m}\right)\)
Nên (a) \(\Leftrightarrow\begin{cases}x-m-\frac{3}{np}\left(y-\frac{3}{m}\right)=0\\x-n-\frac{3}{mp}\left(y-\frac{3}{n}\right)=0\end{cases}\) \(\Leftrightarrow\begin{cases}x-\frac{3}{np}y-m+\frac{9}{mnp}=0\\x-\frac{3}{mp}y-n+\frac{9}{mnp}=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=-\frac{9}{mnp}\\y=-\frac{mnp}{3}\end{cases}\)
Suy ra \(H\left(-\frac{9}{mnp};-\frac{mnp}{3}\right)\)
Vì \(y_H=\frac{3}{x_H}\) nên \(H\in\left(C\right)\)\(\Rightarrow\) điều phải chứng minh
b) \(B\left(b;\frac{2m-b}{b+m}\right)\in\left(C_m\right)\Rightarrow\overrightarrow{AB}=\left(b;\frac{m-2b}{m+b}\right)\)
Ta có : \(I\left(-m;-1\right)\Rightarrow\overrightarrow{AI}=\left(-m;-2\right)\)
Tam giác ABI vuông cân tại A \(\Leftrightarrow\begin{cases}\overrightarrow{AB.}\overrightarrow{AI}=0\\AB^2=AI^2\end{cases}\)
\(\begin{cases}mb+2\frac{m-2b}{m+b}=0\\m^2+4=b^2+\left(\frac{m-2b}{m+b}\right)^2\end{cases}\)\(\Leftrightarrow\begin{cases}\frac{m-2b}{m+b}=-\frac{bm}{2}\left(1\right)\\m^2+4=b^2+\frac{m^2b^2}{4}\left(2\right)\end{cases}\)
\(\left(2\right)\Leftrightarrow m^2\left(b^2-4\right)+4\left(b^2-4\right)=0\Leftrightarrow\left(b^2-4\right)\left(m^2+4\right)=0\)
\(\Leftrightarrow b^2=4\Leftrightarrow b=\pm2\)
* b = 2 thay vào (1) ta được \(\frac{m-4}{m+2}=-m\Leftrightarrow m^2+3m-4=0\Leftrightarrow m=1;m=-4\)
* b = - 2 thay vào (1) ta được \(\frac{m+4}{m-2}=m\Leftrightarrow m^2-3m-4=0\Leftrightarrow m=-1;m=4\)
Vậy \(m=\pm1;m=\pm4\) là những giá trị cần tìm