Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường thẳng
d m x = 1 + 2 t y = 1 - m t , t ∈ R z = - 2 + m t đi qua điểm cố định M ( 1;0;-2 )
Vậy khoảng cách từ O tới d m là h < O M để khoảng cách này đạt giá trị lớn nhất bằng OM
⇒ O M 1 ; 0 ; - 2 ⊥ u 2 ; 1 ; - m ; m ⇔ 2 - 2 m = 0 ⇒ m = 1
Đáp án cần chọn là C

Ta có Pt d2 :x+2y-5=0
vì M ϵ d1 :x-y-1=0 nên M(m,m-1)
MA2 = (-1-m)2 + (2-m+1)2 = 1+2m+m2 +9-6m+m2 =2m2 -4m+10
<=> MA=\(\sqrt{2m^2-4m+10}\)
d(m,d2 )= \(\frac{\left|m+2m-2-5\right|}{\sqrt{1^2+2^2}}\) =\(\frac{\left|3m-7\right|}{\sqrt{5}}\)
theo bài ra thì MA=d(M,d2)
=>\(\frac{\left|3m-7\right|}{\sqrt{5}}\)=\(\sqrt{2m^2-4m+10}\) <=>|3m-7|=\(\sqrt{5}\)\(\sqrt{2m^2-4m+10}\)
<=>9m2 -42m +49=5(2m2-4m+10)
<=>9m2 -42m +49=10m2 -20m +50
<=>m2 +22m +1=0
<=>m= -11+2\(\sqrt{30}\) hoặc m=-11-2\(\sqrt{30}\)
=> M(-11+2\(\sqrt{30}\) ,-12+2\(\sqrt{30}\) ) hoặc M(-11-2\(\sqrt{30}\) ,-12-2\(\sqrt{30}\) )

Ta có phương trình tham số của d là:
d : x - 3 2 = y + 2 1 = z + 1 - 1
Suy ra tọa độ điểm M là nghiệm của phương trình:
3 + 2t - 2 + t - 1 - t + 2 = 0 nên t = -1 nên M ( 1;-2;0 )
Lại có VTPT của (P) là n P → 1 ; 1 ; 1 , VTCP của d là u d → 2 ; 1 ; - 1
Vì ∆ nằm trong (P) và vuông góc với d nên VTCP u ∆ → = u d → ; n p → = 2 ; 3 ; - 1
Gọi N ( x;y;z ) là hình chiếu vuông góc của M trên ∆ , khi đó M N → x - 1 ; y + 3 ; z
Ta có M N → vuông góc với u ∆ → nên ta có hệ phương trình: 2x - 3y + z - 11 = 0
Lại có N ∈ P và MN = 42 ta có hệ:
x + y + z = 2 2 x - 3 y + z - 11 = 0 x - 1 2 + y - 3 2 + z 2 = 42
Giải hệ ta tìm được hai nghiệm ( x;y;z ) là ( 5;-2;-5 ) và ( -3;-4;5 )
- Nếu N ( 5;-2;-5 ) ta có phương trình
∆ : x - 5 2 = y + 2 - 3 = z + 5 1
- Nếu N ( -3;-4;5 ) ta có phương trình
∆ = x + 3 2 = y + 4 - 3 = z - 5 1
Đáp án D

\(M>\frac{x}{x+y+z+t}+\frac{y}{x+y+z+t}+\frac{z}{x+y+z+t}+\frac{t}{x+y+z+t}=\frac{x+y+z+t}{x+y+z+t}=1\)
Mà \(\frac{a}{b}<1\) thì \(\frac{a}{b}<\frac{a+m}{b+m}\) ; \(m\in N\)*
Do đó \(M<\frac{x+t}{x+y+z+t}+\frac{y+z}{x+y+z+t}+\frac{z+x}{x+y+z+t}+\frac{t+y}{x+y+z+t}=\frac{2\left(x+y+z+t\right)}{x+y+z+t}=2\)
Vậy 1 < M < 2 nên M không phải là số tự nhiên/


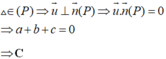


Đáp án C