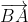Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

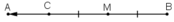
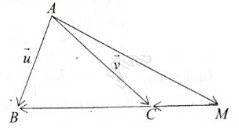
– Trên đoạn MA, lấy điểm C sao cho MC = MB
Nhận thấy 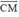 và
và 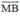 cùng hướng nên
cùng hướng nên 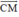 =
= 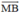
Khi đó:
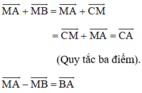

Tham khảo:

a) M thuộc cạnh BC nên vectơ \(\overrightarrow {MB} \) và \(\overrightarrow {MC} \) ngược hướng với nhau.
Lại có: MB = 3 MC \( \Rightarrow \overrightarrow {MB} = - 3.\overrightarrow {MC} \)
b) Ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \)
Mà \(BM = \dfrac{3}{4}BC\) nên \(\overrightarrow {BM} = \dfrac{3}{4}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {BC} \)
Lại có: \(\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \) (quy tắc hiệu)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)
Vậy \(\overrightarrow {AM} = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)

Sao cho \(NB=1 \ cm\) chứ nhỉ? \(AM=2 \ cm; MB=1 \ cm\) thì \(AB=3 \ cm\) à?? !!!

ta có: I là trung điểm của AB
=>\(IA=IB=\dfrac{AB}{2}\)
M là trung điểm của IB
=>\(MI=MB=\dfrac{IB}{2}=\dfrac{AB}{4}\)
AM=AI+IM=1/2AB+1/4AB=3/4AB
=>AM=MB
=>\(\overrightarrow{AM}=3\overrightarrow{MB}\)
=>\(\overrightarrow{AM}-3\overrightarrow{MB}=\overrightarrow{0}\)
=>\(\overrightarrow{AM}+3\overrightarrow{BM}=\overrightarrow{0}\)
=>Chọn C

Ta có: \(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\)
\(\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow-\overrightarrow{MB}=3\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BC}\). Mà \(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\) nên \(\overrightarrow{BM}=\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
Theo quy tắc 3 điểm, ta có
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\Rightarrow\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}-\dfrac{3}{2}\overrightarrow{AB}\)
\(\Rightarrow\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\) hay \(\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{u}+\dfrac{3}{2}\overrightarrow{v}\)

A B C D I K
a)
- \(\overrightarrow{BI}=\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\) (t/c trung điểm)
\(=\frac{1}{2}\left(\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC}\right)\)
\(=\frac{1}{2}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}\)
- \(\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}\)
\(=\overrightarrow{BA}+\frac{1}{3}\overrightarrow{AC}\)
\(=\overrightarrow{BA}+\frac{1}{3}\left(\overrightarrow{BC}-\overrightarrow{BA}\right)\)
\(=\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}-\frac{1}{3}\overrightarrow{BA}\)
\(=\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}\)
b) Ta có: \(\overrightarrow{BK}=\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}=\frac{4}{3}\left(\frac{1}{2}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}\right)=\frac{4}{3}\overrightarrow{BI}\)
=> B,K,I thẳng hàng
c) \(27\overrightarrow{MA}-8\overrightarrow{MB}=2015\overrightarrow{MC}\)
\(\Leftrightarrow27\left(\overrightarrow{MC}+\overrightarrow{CA}\right)-8\left(\overrightarrow{MC}+\overrightarrow{CB}\right)=2015\overrightarrow{MC}\)
\(\Leftrightarrow27\overrightarrow{MC}+27\overrightarrow{CA}-8\overrightarrow{MC}-8\overrightarrow{CB}-2015\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow-1996\overrightarrow{MC}+27\overrightarrow{CA}-8\overrightarrow{CB}=\overrightarrow{0}\)
\(\Leftrightarrow1996\overrightarrow{CM}=8\overrightarrow{CB}-27\overrightarrow{CA}\)
\(\Leftrightarrow\overrightarrow{CM}=\frac{8\overrightarrow{CB}-27\overrightarrow{CA}}{1996}\)
Vậy: Dựng điểm M sao cho \(\overrightarrow{CM}=\frac{8\overrightarrow{CB}-27\overrightarrow{CA}}{1996}\)
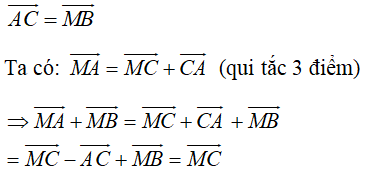
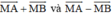
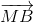 = 3
= 3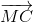 =>
=> 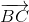 )
)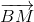 =
= 
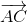 -
- 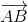 nên
nên 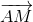 =
= 

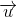 +
+ 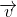
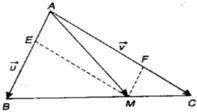
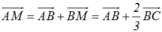
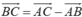
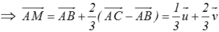
Trên đoạn thẳng AB ta lấy điểm M’ để có =
= 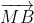
Như vậy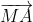 +
+ 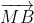 =
= 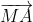 +
+  =
= 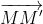 ( quy tắc 3 điểm)
( quy tắc 3 điểm)
Vậy vec tơ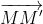 chính là vec tơ tổng của
chính là vec tơ tổng của 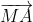 và
và 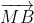
Ta lại có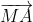 –
– 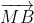 =
= 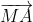 + (-
+ (- 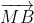 )
)
Theo tính chất giao hoán của tổng vectơ ta có
Vậy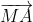 –
– 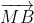 =
=