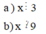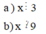
a) A chia h...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. Ta thấy \(12⋮3\\
15⋮3\\
21⋮3\) Để \(A⋮3\) thì \(x⋮3\) Để \(A⋮̸3\) thì \(x⋮̸3\) Để \(A⋮3\Rightarrow12+15+21+x⋮3\) Mà : \(12⋮3\) ; \(15⋮3\) ; \(21⋮3\) \(\Rightarrow x⋮3\left(x\in N\right)\Rightarrow x=3k\left(k\in N\right)\) Để \(A⋮̸\) 3 \(\Rightarrow12+15+21+x⋮̸\) 3 \(\left(x\in N\right)\) Mà : \(12⋮3\) ; \(15⋮3\) ; \(21⋮3\) \(\Rightarrow x⋮̸\) 3 \(\Rightarrow x=3k+r\left(r\in\left\{1;2\right\}\right)\) Vậy ... Để A chia hết cho 3 thì: \(1212+15+21+x⋮3\) Mà: 1212,15,21 đều chia hết cho 3 nên x cũng chia hết cho 3. \(\Rightarrow x\in B\left(3\right)\) Như vậy để x không chia hết cho 3 thì: \(\Rightarrow x\in B\left(3k+1\right),x\in\left(3k+2\right)\)
K
Khách
CM
Cao Minh Tâm
17 tháng 12 2017
Đúng(0)
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MV
18 tháng 5 2017
18 tháng 5 2017
1 tháng 9 2016
