Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có \(\left(log^b_a+log^a_b+2\right)\left(log^b_a-log_{ab}^b\right).log_b^a-1=\left(log^b_a+log^a_b+2\right)\left(log^b_a.log_b^a-log_{ab}^b.log_b^a\right)-1=\left(log^b_a+log^a_b+2\right)\left(1-\frac{1}{log_b^{ba}}log_b^a\right)-1=\left(log^b_a+log^a_b+2\right)\left(1-\frac{1}{1+log^a_b}log^a_b\right)-1=\left(log^b_a+log^a_b+2\right)\frac{1}{1+log^a_b}-1=\left(log^a_b+\frac{1}{log^a_b}+2\right)\frac{1}{1+log^a_b}-1=\frac{\left(1+log^a_b\right)^2}{log^a_b}\frac{1}{1+log^a}-1=\frac{1+log^a_b}{log_b^a}-1=\frac{1}{log_b^a}\)
ta có:
\(\left(log^b_a+\frac{1}{log^b_a}+2\right)\left(log^b_a-\frac{1}{log^{ab}_a}\right)log^a_b-1\)\(=\frac{\left(log^b_a+1\right)^2}{log^b_a}\left(log^b_a-\frac{1}{1+log^b_a}\right)log^a_b-1\)\(=\frac{\left(log^b_a+1\right)^2}{log^b_a}\left(1-\frac{log^a_b}{1+log^b_a}\right)-1\)\(==\frac{\left(log^b_a+1\right)^2}{log^b_a}\left(\frac{1}{1+log^b_a}\right)-1=\frac{1+log^b_a}{log^b_a}-1=\frac{1}{log^b_a}\)


ta áp dụng công thức \(log_a^{x_1x_2...x_n}=log_a^{x_1}+log_a^{x_2}+...+log_a^{x_n}\) ta có
\(log_2^{600}=log_2^{25.8.3}=log_2^{25}+log_2^8+log_2^3=2log_2^5+3+log_2^3=2b+3+a\)

ta có
\(\)\(y=\frac{1}{3}\log^3_{\frac{1}{2}}x+\log^2_{\frac{1}{2}}x-3\log_{\frac{1}{2}}x+1\)
Đặt =\(t=\log_{\frac{1}{2}}x\) ta có
\(y=\frac{1}{3}t^3+t^2-3t+1\)
với \(\frac{1}{4}\le x\le4\Leftrightarrow\frac{1}{4}\le\left(\frac{1}{2}\right)^t\le4\Leftrightarrow-2\le t\le2\)
thay vì tính GTLN,GTNN của hàm số y trên [1/4;4] ta tính GTLN,GTNN của hàm số trên [-2;2]
ta tính \(y'=t^2+2t-3\)
ta tính y'=0 suy ra t=1(loại);t=-3(loại)
ta tính y(2)=\(\frac{5}{3}\);y(-2)=\(\frac{-25}{3}\)
vậy GTNN của y=\(\frac{-25}{3}khi\log_{\frac{1}{2}}x=-2\Rightarrow x=4\)
hàm số đạt GTLN y=\(\frac{5}{3}\) khi \(\log_{\frac{1}{2}}x=2\Leftrightarrow x=\left(\frac{1}{2}\right)^2=\frac{1}{4}\)

ta có \(log^{27}_2=log^{3^3}_2=3log^3_2=a\Rightarrow log^3_2=\frac{a}{3}\)
mặt khác
\(log^{\sqrt[6]{2}}_{\sqrt{3}}=\frac{1}{log^{\sqrt{3}}_{\sqrt[6]{2}}}=\frac{1}{log^{3^{\frac{1}{2}}}_{2^{\frac{1}{6}}}}=\frac{1}{\frac{1}{2}log^3_{2^{\frac{1}{6}}}}=\frac{1}{\frac{1}{2}\frac{1}{\frac{1}{6}}log_2^3}=\frac{1}{3.log_2^3}=\frac{1}{3}.\frac{a}{3}=\frac{a}{9}\)

ta có:
\(log^{\left(2a^2\right)}_2+\left(log_2^a\right)a^{log_a^{\left(log^a_1+1\right)}}+\frac{1}{2}log^2_2a^4=log_2^2+log_2^{a^2}+log_2^a\left(log^a_2+1\right)+\frac{1}{2}log^2_2a^4\)
\(=1+2log^a_2+log^a_2\left(1+log^a_2\right)+2log^2a_2\)
\(=3log^2_2a+3log^a_2+1\)
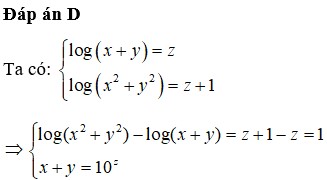
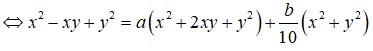
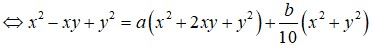
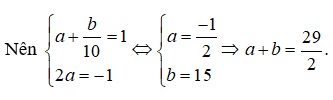
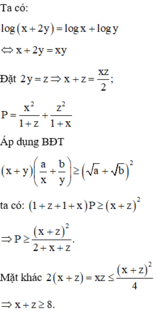
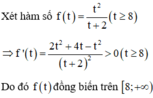
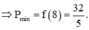
Đáp án B
Diện tích tam giác A B C : S A B C = 1 2 . A B . A C . sin A ^ = 3 a 2 4
Có B C = A B 2 + A C 2 − 2. A B . A C . c o s B A C ^ = a 3
Ta có A B ' = a 2 + a 2 = a 2 , A I = a 2 + a 2 2 = a 5 2
Ta được A B ' 2 + A I 2 = 2 a 2 + a 5 2 2 = 13 a 2 4 = B ' I 2 . Suy ra tam giác AB’I vuông tại A, có diện tích bằng: S A B I = 1 2 . A B ' . A I = 1 2 a 2 . a 5 2 = a 2 10 4
Tam giác ABC là hình chiếu vuông góc của tam giác AB’I trên A B C nên ta có:
S A B C = c o s α . S A B ' I ⇔ c o s α = a 2 3 4 : a 2 10 4 = 30 10
Chú ý: Nếu không được “may mắn có Δ A B ' I vuông”, ta có thể sử dụng công thức He-rông để tính diện tích tam giác A B ' I