Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi S’ là giá trị của S khi giảm đi 16 lần, x’ là cạnh hình lập phương khi S giảm đi 16 lần.
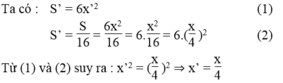
Vậy khi S giảm đi 16 lần thì cạnh hình vuông giảm đi 4 lần.

a, \(S_{tp}=x^2+x^2+...=6x^2\)
b, ( Cái này chắc thay vô r bấm máy nha :vvvv )
c, Ta có : \(S_{tpm}=54x_2^2=6x^2_1\)
\(\Leftrightarrow x^2_1=9x^2_2\)
\(\Leftrightarrow x_1=3x_2\)
Vậy để S tăng 9 lần thì x phải tăng 3 lần .
d, TH1 : S = 37,5 cm2 .
\(\Leftrightarrow6x^2=37,5\)
\(\Leftrightarrow x=\dfrac{5}{2}\left(cm\right)\)
TH2 : S = 24 cm2 .
\(\Leftrightarrow6x^2=24\)
\(\Leftrightarrow x=2\)
Vậy ...

Giá trị của S và x được thể hiện trong bảng sau:
| x | 1/3 | 1/2 | 1 | 3/2 | 2 | 3 |
| S | 2/3 | 3/2 | 6 | 27/2 | 24 | 54 |

Ta thấy ngay cạnh của hình lập phương gấp đôi bán kính hình cầu
a) Tỉ số cần tính \(\dfrac{6}{\pi}\)
b) Diện tích toàn phần của hình lập phương là \(42cm^2\)
c) Thể tích cần tính xấp xỉ \(244cm^3\)

Hình như đề sai nha bạn
khi đó x + y + z = 1 ; x3 + y3 + z3 = 3
mà (x + y + z)3 = x3 + y3 + z3 + 3(x + y)(y + z)(z + x)
<=> 13 = 3 + 3(x + y)(y + z)(z + x)
<=> 3(x + y)(y + z)(z + x) = -2 (vô lý vì 3(x + y)(y + z)(z + x) > 0)
Iuukweewddukhkhuckekwhkuekcwuhwdikeuldkhscuhkjdcshudscjhukidschfshjrskdhjfursiuhukerfhevkhgyrukeaguukeeafduuhkafeuiehfugkurfrfaegukurgfeuwukfegukuqrfrekgquufrequgkuefqehhmeihuewkfkihurfewuhkifrekwhhubrhefjwkhjbkefeqhebfeqkehbfjkeahejchkeajhhkeceahjbkceeabhjrevahkbjreahhjvjbhkvfhhjkfvsrhhkjbhkrjfeahjhkvreajhbkvesrhvbjerahjbkrfeajhhkefrahhikferahhkjfreahhrfeajfrehuiqkrhehiakfhfhhrefkiuahiukrfea

Diện tích hình vuông cạnh c là \(S=c^2\)
Tổng diện tích hai hình chữ nhật là \(S_1=2ab\)
Xét tg vuông có \(c^2=a^2+b^2\)
Áp dụng cosi có
\(\frac{a+b}{2}\ge\sqrt{ab}\Rightarrow\frac{a^2+b^2+2ab}{4}\ge ab\Rightarrow a^2+b^2\ge2ab\) Dấu = xảy ra khi \(a=b\)
\(\Rightarrow S\ge S_1\left(dpcm\right)\)
\(S=S_1\) Khi a=b => tg ban đầu phải là tg vuông cân

Diện tích của một mặt hình lập phương là x 2
Hình lập phương có 6 mặt nên có diện tích toàn phần 6 x 2