Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

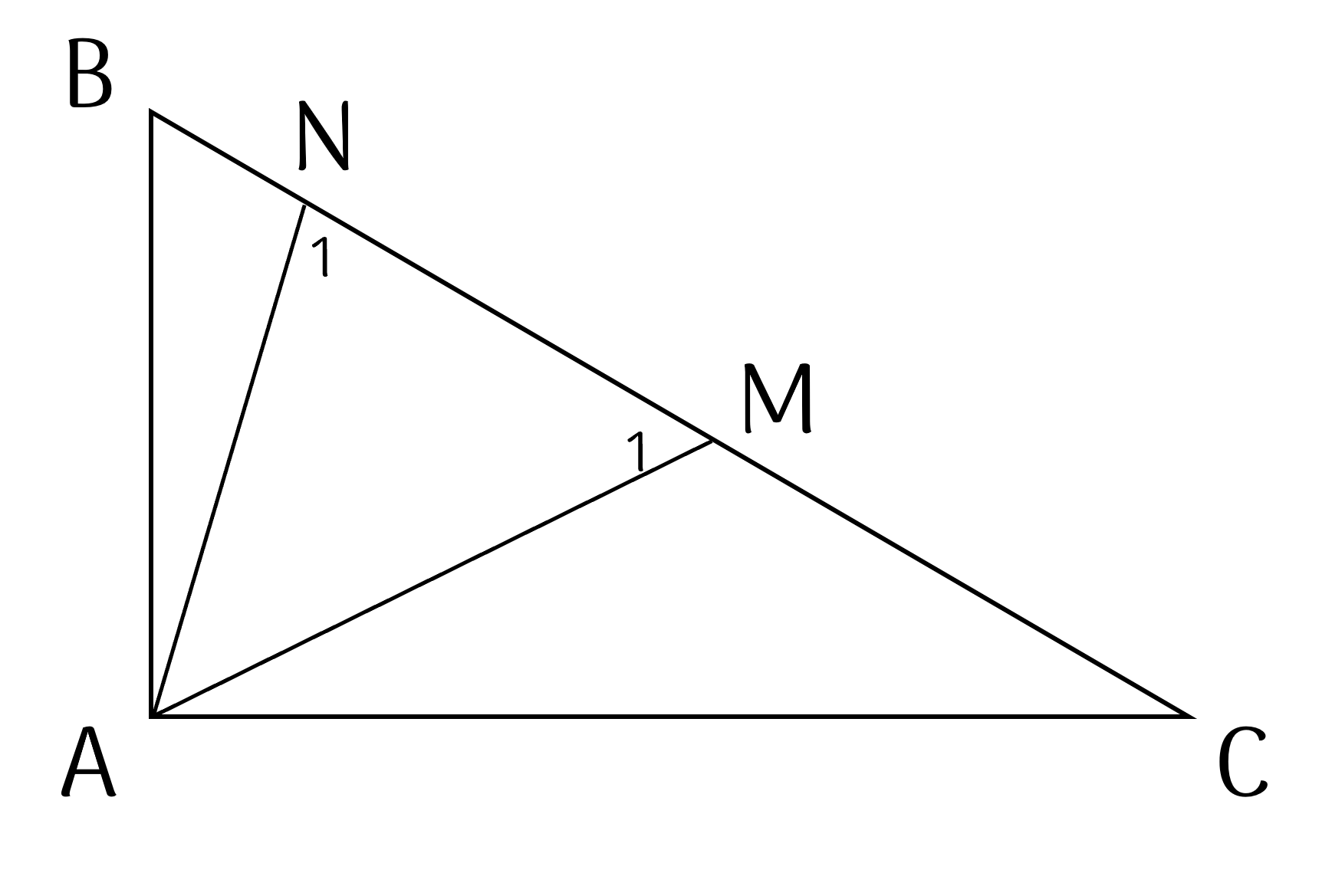
$BM = BA$ nên $\Delta BAM$ cân tại $B$.
Suy ra $\widehat{M_1} = \dfrac{180^{\circ} - \widehat{B}}2$.
$CN = CA$ nên $\Delta CAN$ cân tại $C$.
Suy ra $\widehat{N_1} = \dfrac{180^{\circ} - \widehat{C}}2$.
Suy ra $\widehat{N_1} + \widehat{M_1} = 180^{\circ} - \dfrac12(\widehat{B} + \widehat{C})$
nên $180^{\circ} - \widehat{N_1} - \widehat{M_1} = \dfrac12(\widehat{B} + \widehat{C})$
Trong $\Delta MAN$ có $\widehat{MAN} = 180^{\circ} - \widehat{N_1} - \widehat{M_1}$
nên $\widehat{MAN} = \dfrac12(\widehat{B} + \widehat{C}) = \dfrac12.90^{\circ} = 45^{\circ}$.

Chia \(n^3-n^2+2n+7\) cho \(n^2+1\) , được \(n-1,\) dư \(n+8\)
\(n+8⋮n^2+1\)
\(\Rightarrow\left(n+8\right)\left(n-8\right)=n^2-64⋮n^2+1\)
\(\Rightarrow n^2+1-65⋮n^2+1\Rightarrow65⋮n^2+1\)
Lần lượt cho \(n^2+1\) bằng \(1;5;13;65\) được n bằng \(0;\pm2;\pm8\)

A B C M N
Ta có
BM=AB suy ra tam giác BAM cân tại B suy ra \(\widehat{BAM}=\frac{180^o-\widehat{B}}{2}\)
CN=AC suy ra tam giác NAC cân tại C suy ra \(\widehat{NAC}=\frac{180^o-\widehat{C}}{2}\)
(nếu cần thì bạn phải cm thêm cả N nằm giữa B và M nhé!)
MÀ ta thấy \(\widehat{BAM}+\widehat{ACN}=\widehat{BAC}+\widehat{NAM}\)
\(\Rightarrow\frac{180^o-\widehat{B}}{2}+\frac{180^o-\widehat{C}}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-\left(\widehat{B}+\widehat{C}\right)}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-90^o}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\widehat{NAM}=45^o\)

.
.
.nônnonononononnnnonnnononnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnooooooooooooooooo
.
.
.

a, theo pytago ta có:
AB2+AC2=BC2 <=> AC=\(\sqrt{10^2-6^2}\)=8 (cm)
so sánh: BAC>ABC>ACB vì BC>AC>AB
b, vì A là trung điểm BD nên CA là trung tuyến của tam giác DBC
mà CA\(\perp\)BD nên CA là đường cao của tam giác DBC
=> CA vừa là trung tuyến vừa là đường cao của tam giác DBC nên DBC cân ở C