Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ AE vuông góc SC (E thuộc SC)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\)
\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\Rightarrow SC\perp\left(AMN\right)\)
Mà \(AE\perp SC\Rightarrow E\in\left(AMN\right)\)
\(\Rightarrow AE\) là hình chiếu vuông góc của SA lên (AMN)
\(\Rightarrow\widehat{SAE}\) là góc giữa SA và (AMN)
\(AC=a\sqrt{2}\Rightarrow SC=\sqrt{SA^2+AC^2}=2a\)
\(\Delta SAC\) vuông cân tại A \(\Rightarrow AE=SE=\dfrac{1}{2}SC=a\)
\(\Rightarrow\Delta SAE\) vuông cân tại E \(\Rightarrow\widehat{SAE}=45^0\)

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\) (1)
Tam giác SAB vuông cân tại A (do SA=SB=a)
\(\Rightarrow AM\perp SB\) (trung tuyến đồng thời là đường cao) (2)
(1);(2)\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\)
\(\Rightarrow SC\perp\left(AMN\right)\Rightarrow\left(SAC\right)\perp\left(AMN\right)\)
Từ A kẻ \(AH\perp SC\Rightarrow H\in\left(AMN\right)\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{HAC}\) là góc giữa (AMN) và (ABCD)
\(AC=a\sqrt{2}\) ; \(SC=a\sqrt{3}\)
\(sin\widehat{HAC}=cos\widehat{SCA}=\dfrac{AC}{SC}=\sqrt{\dfrac{2}{3}}\Rightarrow\widehat{HAC}\approx54^044'\)

Chọn đáp án A
+ Ta có
![]()
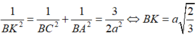
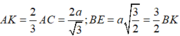
nên K là trọng tâm của tam giác BCD
+ Ta dễ dàng chứng minh được SH ⊥ (BKH) ⇒ SB, (BKH) = SBH
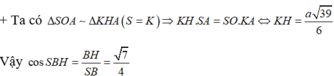

+)CD⊥SA do SA vuông với ABCD
CD⊥AD( tính chất hình vuông)
=>CD⊥(SAD)=>CD⊥AN mà SD⊥AN=> AN⊥(SDC)=>AN⊥SC(1)
+) BC⊥SA do SA vuông với ABCD
BC⊥AB( tính chất hình vuông)
=>BC⊥(SAB)=>BC⊥AM mà SB⊥AM=> AM⊥(SAB)=>AM⊥SC(2)
TỪ 1 và 2 => SC⊥(AMN) đpcm

a: \(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1/căn 2
=>góc SCA=35 độ
b:
Kẻ BH vuông góc AC tại H
(SB;SAC)=(SB;SH)=góc BSH
\(HB=\dfrac{a\cdot a}{a\sqrt{2}}=a\cdot\dfrac{\sqrt{2}}{2}\)
AH=AC/2=a*căn 2/2
=>\(SH=\sqrt{a^2+\dfrac{1}{2}a^2}=a\sqrt{\dfrac{3}{2}}\)
\(SH=\dfrac{a\sqrt{6}}{2};HB=\dfrac{a\sqrt{2}}{2};SB=a\sqrt{2}\)
\(cosBSH=\dfrac{SB^2+SH^2-BH^2}{2\cdot SB\cdot SH}=\dfrac{\sqrt{3}}{2}\)
=>góc BSH=30 độ
c: (SD;(SAB))=(SD;SA)=góc ASD
tan ASD=AD/AS=2
nên góc ASD=63 độ
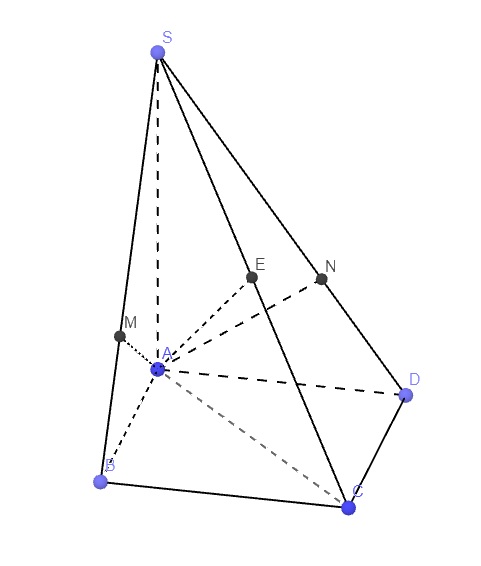


A B C D S O M N P Q
Lấy P thuộc SC sao cho \(AP\perp SC\)
Ta có: \(\hept{\begin{cases}BC\perp AB\\BC\perp AS\end{cases}\Rightarrow BC\perp\left(SAB\right)\Rightarrow AM\perp BC}\)
\(\hept{\begin{cases}AM\perp BC\\AM\perp SB\end{cases}}\Rightarrow AM\perp\left(SBC\right)\Rightarrow SC\perp AM\)
Tương tự \(SC\perp AN\). Do đó \(SC\perp MAN\)
Vì \(AP\perp SC\)nên P nằm trong mặt phẳng (AMN) hay \(CS\perp\left(AMN\right)\)tại P
Lại có: CA cắt (AMN) tại A, O là trung điểm của CA. Suy ra:
\(d\left(O;AMN\right)=\frac{1}{2}d\left(C,AMN\right)=\frac{CP}{2}=\frac{CA^2}{2CS}=\frac{\left(a\sqrt{2}\right)^2}{2\sqrt{\left(2a\right)^2+\left(a\sqrt{2}\right)^2}}=\frac{\sqrt{6}a}{6}\)