Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc ô tô dự định đi quãng đường AB là x (km/h).
Có phương trình: 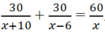
Giải ra được x = 30
Thời gian ô tô dự định đi là 2 giờ.

gọi vận tốc dự định là :x>0
vận tốc khi tăng tốc là : x+10
thời gian dự kiến là : 120:x
thời gian thực tế là : 120 :(x+10)
ta có: \(\frac{120}{x+10}+0,6=\frac{120}{x}\Leftrightarrow0,6x^2+6x-1200=0\Leftrightarrow\orbr{\begin{cases}x=40\\x=-50\end{cases}}\)
kết hợp điều kiện có vận tốc dự kiến của xe là 40km/h

Giải:
Gọi vận tốc dự định đi quãng đường AB = x km/giờ (x>0)
thời gian dự định đi quãng đường AB = 60/x
--> vận tốc đi nửa đường đầu (đi 30km đầu) = x + 10
thời gian đi nửa đường đầu = 30/(x + 10)
--> vận tốc đi nửa đường sau (đi 30 km sau) = x - 6
thời gian đi nửa đường sau = 30/(x -6)
Theo đề ta có
30/(x + 10) + 30/(x - 6) = 60/x
1/(x + 10) + 1/(x - 6) = 2/x
x(x-6) + x(x+10) = 2(x-6)(x+10)
x^2 - 6x + x^2 +10x = 2(x^2 + 4x - 60)
2x^2 + 4x = 2x^2 + 8x - 120
4x = 120
x = 30 (thỏa)
Vậy thời gian dự định đi quãng đường AB là t = 60/x = 60/30 = 2 giờ

A)
Giải:
gọi vận tốc dự định đi quãng đường AB = x km/giờ (x>0)
thời gian dự định đi quãng đường AB = 60/x
--> vận tốc đi nửa đường đầu (đi 30km đầu) = x + 10
thời gian đi nửa đường đầu = 30/(x + 10)
--> vận tốc đi nửa đường sau (đi 30 km sau) = x - 6
thời gian đi nửa đường sau = 30/(x -6)
Theo đề ta có
30/(x + 10) + 30/(x - 6) = 60/x
1/(x + 10) + 1/(x - 6) = 2/x
x(x-6) + x(x+10) = 2(x-6)(x+10)
x^2 - 6x + x^2 +10x = 2(x^2 + 4x - 60)
2x^2 + 4x = 2x^2 + 8x - 120
4x = 120
x = 30 (thỏa)
Vậy thời gian dự định đi quãng đường AB là t = 60/x = 60/30 = 2 giờ

gọi vận tốc dự định đi quãng đường AB = x km/giờ (x>0)
thời gian dự định đi quãng đường AB = 60/x
--> vận tốc đi nửa đường đầu (đi 30km đầu) = x + 10
thời gian đi nửa đường đầu = 30/(x + 10)
--> vận tốc đi nửa đường sau (đi 30 km sau) = x - 6
thời gian đi nửa đường sau = 30/(x -6)
Theo đề ta có
30/(x + 10) + 30/(x - 6) = 60/x
1/(x + 10) + 1/(x - 6) = 2/x
x(x-6) + x(x+10) = 2(x-6)(x+10)
x^2 - 6x + x^2 +10x = 2(x^2 + 4x - 60)
2x^2 + 4x = 2x^2 + 8x - 120
4x = 120
x = 30 (thỏa)
Vậy thời gian dự định đi quãng đường AB là t = 60/x = 60/30 = 2 giờ

gọi thời gian dự định là x
Quãng đường AB là 50x (km)
Quãng đường đã đi đk là 50 \(\frac{2}{3}\)x(km)
Thời gian còn lại là x-\(\frac{2}{3}\)x=\(\frac{1}{3}\)x(km/h)
Quãng đường đi vs vận tốc là 30\(\frac{1}{3}\)x(km)
vì Quãng đường AB k thay đổi nên ta có phương trình :
\(\frac{100}{3}\)x+10x+48=50x
\(\frac{100}{3}\)x+\(\frac{30}{3}\)x+\(\frac{144}{3}\)x=\(\frac{150}{3}\)x
100x+30x+144=150x
20x=144
x=7,2
Quãng đường AB là 7,2 . 50 = 360 (km)

Đổi : 60m = 0,06km
- Gọi vận tốc dự định đi là x ( km/h, x > 0 )
- Vận tốc thức tế ở hai nửa quãng đường là : x + 10; x - 6 ( km/h )
Theo bài ra ta có : \(\dfrac{0,03}{x+10}+\dfrac{0,03}{x-6}=\dfrac{0,06}{x}\)
\(\Leftrightarrow\dfrac{1}{x+10}+\dfrac{1}{x-6}=\dfrac{2}{x}\)
\(\Leftrightarrow x\left(x-6\right)+x\left(x+10\right)=2\left(x+10\right)\left(x-6\right)\)
\(\Leftrightarrow4x=120\)
\(\Leftrightarrow x=30\) ( TM )
Vậy ...
Gọi vận tốc dự định của ô tô là x(km/h)(Điều kiện: x>0)
Theo đề, ta có phương trình:
\(\dfrac{30}{x+10}+\dfrac{30}{x-6}=\dfrac{60}{x}\)
\(\Leftrightarrow\dfrac{30\left(x-6\right)+30\left(x+10\right)}{\left(x+10\right)\left(x-6\right)}=\dfrac{60}{x}\)
\(\Leftrightarrow\dfrac{30x-180+30x+300}{\left(x+10\right)\left(x-6\right)}=\dfrac{60}{x}\)
\(\Leftrightarrow x\left(60x+120\right)=60\left(x+10\right)\left(x-6\right)\)
\(\Leftrightarrow60x^2+120x=60\left(x^2-6x+10x-60\right)\)
\(\Leftrightarrow60x^2+120x=60x^2+240x-3600\)
\(\Leftrightarrow-120x=-3600\)
hay x=30(thỏa ĐK)
Vậy: Vận tốc dự định là 30km/h

Gọi vận tốc của ô tô dự định là x (x>6)
=> Thời gian dự định là \(\frac{60}{x}\)
Nửa quãng đường đầu dài 30 km
Vận tốc đi nửa quãng đường đầu là x+10
=> Thời gian đi nửa quãng đường đầu là \(\frac{30}{x+10}\)
Vận tốc đi nửa quãng đường sau là x−6
=> Thời gian đi nửa quãng đường sau là \(\frac{30}{x-6}\)
Theo bài ra ta có phương trình:
\(\frac{30}{x+10}+\frac{30}{x-6}=\frac{60}{x}\)
Tự giải pt ra được x = 30 (TMĐK)
=> Thời gian ô tô dự định đi quãng đường AB là: \(\frac{60}{30}\)= 2h (CT tính thời gian = quãng đường/ vận tốc)
Gọi vận tốc dự định của ô tô là \(x\left(km/h,x>10\right)\)(Tại sao \(x>10\)? Vì đề bài cho lúc sau vận tốc giảm đi 10km/h nên nếu vận tốc ban đầu mà nhỏ hơn hoặc bằng 10 km/h thì ô tô sẽ không thể tới nơi)
Thời gian dự định ô tô cần đi từ A đến B là \(\frac{180}{x}\left(h\right)\)
Vận tốc lúc sau là \(x-10\left(km/h\right)\)
Thời gian thực tế ô tô dành ra để đi từ A đến B là \(\frac{180}{x-10}\left(h\right)\)
Vì thực tế ô tô đến B muộn hơn dự định 15 phút \(=\frac{1}{4}h\)nên ta có phương trình:
\(\frac{180}{x-10}-\frac{180}{x}=\frac{1}{4}\)\(\Leftrightarrow\frac{180x-180\left(x-10\right)}{x\left(x-10\right)}=\frac{1}{4}\)\(\Leftrightarrow\frac{180x-180x+1800}{x^2-10x}=\frac{1}{4}\)
\(\Leftrightarrow\frac{1800}{x^2-10x}=\frac{1}{4}\)\(\Rightarrow x^2-10x=7200\)\(\Leftrightarrow x^2-10x-7200=0\)\(\Leftrightarrow x^2+80x-90x-7200=0\)\(\Leftrightarrow x\left(x+80\right)-90\left(x+80\right)=0\)
\(\Leftrightarrow\left(x+80\right)\left(x-90\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x+80=0\\x-90=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=-80\left(loại\right)\\x=90\left(nhận\right)\end{cases}}\)
Vậy vận tốc dự định của ô tô là 90km/h
Hỏi em một câu: Tính số tiền bị phạt cho cảnh sát giao thông của tài xế ô tô đó?