Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\dfrac{-36}{63};\dfrac{56}{63};\dfrac{-30}{63}\)
b)\(\dfrac{110}{264};\dfrac{21}{264}\)

a) \(\dfrac{11}{21}+\dfrac{-4}{7}=\dfrac{11}{21}+\dfrac{-12}{21}=\dfrac{-1}{21}\)
b) \(\dfrac{5}{15}+\dfrac{14}{25}-\dfrac{12}{9}+\dfrac{2}{7}+\dfrac{11}{25}=\dfrac{1}{3}+\dfrac{14}{25}-\dfrac{4}{3}+\dfrac{2}{7}+\dfrac{11}{25}\)
\(=\left(\dfrac{1}{3}-\dfrac{4}{3}\right)+\left(\dfrac{14}{25}+\dfrac{11}{25}\right)+\dfrac{2}{7}=-1+1+\dfrac{2}{7}=\dfrac{2}{7}\)
c) \(\dfrac{2}{3}+\dfrac{5}{7}-\dfrac{3}{14}=\dfrac{28}{42}+\dfrac{30}{42}-\dfrac{9}{42}=\dfrac{49}{42}=\dfrac{7}{6}\)
d) \(\dfrac{2}{5}-\dfrac{3}{7}+\dfrac{9}{45}=\dfrac{2}{5}-\dfrac{3}{7}+\dfrac{1}{5}=\dfrac{14}{35}-\dfrac{15}{35}+\dfrac{7}{35}=\dfrac{6}{35}\)
e) \(\dfrac{21}{47}+\dfrac{9}{45}+\dfrac{26}{47}+\dfrac{45}{5}=\dfrac{21}{47}+\dfrac{1}{5}+\dfrac{26}{47}+\dfrac{45}{5}=\left(\dfrac{21}{47}+\dfrac{26}{47}\right)+\left(\dfrac{1}{5}+\dfrac{45}{5}\right)\)
\(=1+\dfrac{46}{5}=\dfrac{51}{5}\)
f) \(\dfrac{15}{12}-\dfrac{18}{13}+\dfrac{5}{13}-\dfrac{3}{12}=\left(\dfrac{15}{12}-\dfrac{3}{12}\right)+\left(-\dfrac{18}{13}+\dfrac{5}{13}\right)=1+\left(-1\right)=0\)
g) \(\dfrac{-8}{18}-\dfrac{15}{27}=\dfrac{-4}{9}-\dfrac{5}{9}=\dfrac{-9}{9}=-1\)
h)\(\dfrac{3}{7}+\dfrac{-5}{2}-\dfrac{3}{5}=\dfrac{30}{70}+\dfrac{-175}{70}-\dfrac{42}{70}=\dfrac{-187}{70}\)
i) \(\left(\dfrac{11}{12}:\dfrac{33}{16}\right).\dfrac{3}{5}=\dfrac{11}{12}.\dfrac{16}{33}.\dfrac{3}{5}=\dfrac{11.16.3}{12.33.5}=\dfrac{4}{15}\)

a)\(\dfrac{2}{5}-\dfrac{3}{7}+\dfrac{9}{45}\\ =\dfrac{2}{5}-\dfrac{3}{7}+\dfrac{1}{5}\\ =\dfrac{14-15+1}{35}\\ =\dfrac{0}{35}=0\)
b)\(\dfrac{5}{15}+\dfrac{14}{25}-\dfrac{12}{9}+\dfrac{2}{7}+\dfrac{11}{25}\\ =\left(\dfrac{1}{3}-\dfrac{4}{3}\right)+\left(\dfrac{14}{25}+\dfrac{11}{25}\right)+\dfrac{2}{7}\\ =-1+1+\dfrac{2}{7}\\ =0+\dfrac{2}{7}=\dfrac{2}{7}\)

Bài 1: Tính ( hợp lý nếu có thể )
\(A=\dfrac{-3}{8}+\dfrac{12}{25}+\dfrac{5}{-8}+\dfrac{2}{-5}+\dfrac{13}{25}\)
\(=\left(\dfrac{-3}{8}+\dfrac{5}{-8}\right)+\left(\dfrac{12}{25}+\dfrac{13}{25}\right)+\dfrac{2}{-5}\)
\(=-1+1+\dfrac{2}{-5}\)
\(=0+\dfrac{2}{-5}\)
\(=\dfrac{2}{-5}\)
\(B=\dfrac{-3}{15}+\left(\dfrac{2}{3}+\dfrac{3}{15}\right)\)
\(=\left(\dfrac{-3}{15}+\dfrac{3}{15}\right)+\dfrac{2}{3}\)
\(=0+\dfrac{2}{3}\)
\(=\dfrac{2}{3}\)
\(C=\dfrac{-5}{21}+\left(\dfrac{-16}{21}+1\right)\)
\(=\left(\dfrac{-5}{21}+\dfrac{-16}{21}\right)+1\)
\(=-1+1\)
\(=0\)
\(D=\left(\dfrac{-1}{6}+\dfrac{5}{-12}\right)+\dfrac{7}{12}\)
\(=\left(\dfrac{5}{-12}+\dfrac{7}{12}\right)+\dfrac{-1}{6}\)
\(=\dfrac{1}{6}+\dfrac{-1}{6}\)
\(=0\)
Bài 2: Tìm x,biết:
a) \(x+\dfrac{2}{3}=\dfrac{4}{5}\)
\(x=\dfrac{4}{5}-\dfrac{2}{3}\)
\(x=\dfrac{2}{15}\)
Vậy \(x=\dfrac{2}{15}\)
b) \(x-\dfrac{2}{3}=\dfrac{7}{21}\)
\(\Rightarrow x-\dfrac{2}{3}=\dfrac{1}{3}\)
\(x=\dfrac{1}{3}+\dfrac{2}{3}\)
\(x=\dfrac{3}{3}=1\)
Vậy \(x=1\)
c) sai đề hay sao ấy bạn.bỏ dấu - ở x thì đúng đề.mk giải luôn nha!
\(x-\dfrac{3}{4}=\dfrac{-8}{11}\)
\(x=\dfrac{-8}{11}+\dfrac{3}{4}\)
\(x=\dfrac{1}{44}\)
Vậy \(x=\dfrac{1}{44}\)
d) \(\dfrac{11}{12}-\left(\dfrac{2}{5}+x\right)=\dfrac{2}{3}\)
\(\dfrac{2}{5}+x=\dfrac{11}{12}-\dfrac{2}{3}\)
\(\dfrac{2}{5}+x=\dfrac{1}{4}\)
\(x=\dfrac{1}{4}-\dfrac{2}{5}\)
\(x=-\dfrac{3}{20}\)
Vậy \(x=-\dfrac{3}{20}\)

a)\(\dfrac{1212}{2323}=\dfrac{1212:101}{2323:101}=\dfrac{12}{23}\)
b)\(\dfrac{-3435}{4141}< \dfrac{-3434}{4141}=\dfrac{-3434:101}{4141:101}\)
Nhận xét:
\(\dfrac{\overline{abab}}{\overline{cdcd}}=\dfrac{\overline{ab}}{\overline{cd}}\)

\(\dfrac{-14}{21};\dfrac{-2}{15};\dfrac{14}{-35}\)
\(\dfrac{-17}{21}=\dfrac{-85}{105}\);\(\dfrac{-2}{15}=\dfrac{-14}{105};\dfrac{14}{-35}=\dfrac{-14}{35}=\dfrac{-42}{105}\)
\(\dfrac{17}{60};\dfrac{5}{12};\dfrac{64}{90}\)
\(\dfrac{17}{60}=\dfrac{51}{180};\dfrac{-5}{12}=\dfrac{-75}{180};\dfrac{-64}{90}=\dfrac{-32}{45}=\dfrac{-128}{180}\)
bài2:
a)\(\dfrac{3}{5}>\dfrac{4}{7}\)
b)\(\dfrac{-5}{8}< \dfrac{-7}{12}\)
c)\(\dfrac{5}{-3}< \dfrac{-9}{12}\)

Các bạn không cần trả lời câu hỏi trên của mik vì mik đã hiểu rồi nha . Cho nên đừng trả lời ! OK![]()

c) E = \(\dfrac{4116-14}{10290-35}\) và K = \(\dfrac{2929-101}{2.1919+404}\)
E = \(\dfrac{4116-14}{10290-35}\)
E = \(\dfrac{14.\left(294-1\right)}{35.\left(294-1\right)}\)
E = \(\dfrac{14}{35}\)
K = \(\dfrac{2929-101}{2.1919+404}\)
K = \(\dfrac{101.\left(29-1\right)}{101.\left(38+4\right)}\)
K = \(\dfrac{29-1}{34+8}\)
K = \(\dfrac{28}{42}\) = \(\dfrac{2}{3}\)
Ta có : E = \(\dfrac{14}{35}\) và K = \(\dfrac{2}{3}\)
\(\dfrac{14}{35}\) = \(\dfrac{42}{105}\)
\(\dfrac{2}{3}\) = \(\dfrac{70}{105}\)
Vậy E < K
Các câu còn lại tương tự

+) \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^9}\)
\(\Rightarrow2A-A=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^9}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\right)\)
\(\Rightarrow A=1-\dfrac{1}{2^{10}}=\dfrac{2^{10}-1}{2^{10}}\)
Vậy \(A=\dfrac{2^{10}-1}{2^{10}}\)
+) \(F=\dfrac{1}{15}+\dfrac{1}{21}+\dfrac{1}{28}+...+\dfrac{1}{190}\)
\(\Rightarrow\dfrac{1}{2}F=\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+...+\dfrac{1}{380}\)
\(=\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{19.20}=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{19}-\dfrac{1}{20}\)
\(=\dfrac{1}{5}-\dfrac{1}{20}=\dfrac{3}{20}\Rightarrow F=\dfrac{3}{20}:\dfrac{1}{2}=\dfrac{3}{10}\)
Vậy \(F=\dfrac{3}{10}\)
+) \(G=\dfrac{12}{84}+\dfrac{12}{210}+\dfrac{12}{390}+...+\dfrac{12}{2100}\)
\(=\dfrac{4}{28}+\dfrac{4}{70}+\dfrac{4}{130}+...+\dfrac{4}{700}=\dfrac{4}{4.7}+\dfrac{4}{7.10}+...+\dfrac{4}{25.28}\)
\(=\dfrac{4}{3}.\left(\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{25.28}\right)\)
\(=\dfrac{4}{3}.\left(\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{25}-\dfrac{1}{28}\right)\)
\(=\dfrac{4}{3}.\left(\dfrac{1}{4}-\dfrac{1}{28}\right)=\dfrac{4}{3}.\dfrac{3}{14}=\dfrac{2}{7}\)
Vậy \(G=\dfrac{2}{7}\)
\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\)
\(2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^9}\)
\(2A-A=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^9}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\right)\)
\(A=1-\dfrac{1}{2^{10}}=\dfrac{1024-1}{1024}=\dfrac{1023}{1024}\)
\(F=\dfrac{1}{15}+\dfrac{1}{21}+\dfrac{1}{28}+...+\dfrac{1}{190}\)
\(=\dfrac{2}{30}+\dfrac{2}{42}+\dfrac{2}{56}+...+\dfrac{2}{380}\)
\(=\dfrac{2}{5.6}+\dfrac{2}{6.7}+\dfrac{2}{7.8}+...+\dfrac{2}{19.20}\)
\(=2\left(\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{19.20}\right)\)
\(=2\left(\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{19}-\dfrac{1}{20}\right)\)
\(=2\left(\dfrac{1}{5}-\dfrac{1}{20}\right)=2.\dfrac{3}{20}=\dfrac{3}{10}\)
\(G=\dfrac{12}{84}+\dfrac{12}{210}+\dfrac{12}{390}+...+\dfrac{12}{2100}\)
\(=\dfrac{4}{28}+\dfrac{4}{70}+\dfrac{4}{130}+...+\dfrac{4}{700}\)
\(=\dfrac{4}{4.7}+\dfrac{4}{7.10}+\dfrac{4}{10.13}+...+\dfrac{4}{25.28}\)
\(=\dfrac{4}{3}\left(\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+...+\dfrac{1}{25}-\dfrac{1}{28}\right)\)
\(=\dfrac{4}{3}\left(\dfrac{1}{4}-\dfrac{1}{28}\right)\)
\(=\dfrac{4}{3}.\dfrac{3}{14}=\dfrac{2}{7}\)
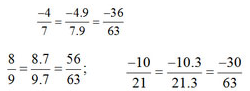
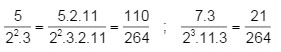
Ta có:
\(\dfrac{21}{3\cdot11}>\dfrac{12}{3\cdot11}\)
\(\dfrac{45}{11\cdot19}>\dfrac{12}{11\cdot19}\)
\(\dfrac{69}{19\cdot27}>\dfrac{12}{19\cdot27}\)
\(\Rightarrow\dfrac{21}{3\cdot11}-\dfrac{45}{11\cdot19}+\dfrac{69}{19\cdot27}>\dfrac{12}{3\cdot11}+\dfrac{12}{11\cdot19}+\dfrac{12}{19\cdot27}\)
\(\Rightarrow A>B\)
Vậy \(A>B\).