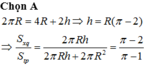Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều dài và chiều rộng lần lượt là \(a,b\left(a,b\in\text{N*}\right)\)
Thửa ruộng có chu vi là \(120m\) \(\Rightarrow2\left(a+b\right)=120\Rightarrow a+b=60\)
Nếu tăng chiều dài thêm 5m và giữ nguyên chiều rộng thì diện tích thửa ruộng tăng thêm 130m2 suy ra \(\left(a+5\right)b=ab+130\)
Hay ta có hệ \(\left\{{}\begin{matrix}a+b=60\\\left(a+5\right)b=ab+130\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a=60-b\\\left(a+5\right)b=ab+130\end{matrix}\right.\)
\(\Rightarrow\left(60-b+5\right)b=\left(60-b\right)b+130\)
\(\Rightarrow65b-b^2=60b-b^2+130\)
\(\Rightarrow5b=130\Rightarrow b=26\) (thỏa)
\(\Rightarrow a=60-b=60-26=34\) (thỏa)
Diện tích thửa ruộng là: \(34\cdot26=884\left(\text{m }^2\right)\)
Gọi chiều dài là a, chiều rộng là b (a,b \(\in\) N*)
Ta có:
2(a+ b) = 120 (*)
(a+5)b = ab + 130
ab + 5b = 130
=> 5b = 130
=> b = 26
Từ (*) => 2(a + 26) = 120
2a + 52 = 120
=> a = 34
Diện tích thửa ruộng: 26.34 = 884 (m2)
Vậy:....

Chọn đáp án A.
Theo giả thiết thể tích khối cầu đá bằng 3 8 - 1 8 = 1 4 thể tích khối trụ.
Do vậy:
4 3 π R 3 = 1 4 π . 0 , 5 2 . 2 ⇒ R = 3 23 3 ⇒ S C = 4 π R 2 ≈ 2 , 6 m 2

Chọn A.
Gọi r là bán kính quả banh. Ta có:
S 1 = 3 4 πr 2 = 12 πr 2
S 2 = 2 πr . 6 r = 12 πr 2

Lời giải:
Xét hình chóp tứ giác đều $S.ABCD$ thì $ABCD$ là hình vuông có cạnh bằng 10 và các cạnh bên bằng nhau.
Gọi độ dài cạnh bên là $a$.
Từ $S$ hạ đường cao $SH$ xuống hình chóp thì $H$ chính là tâm của hình vuông $ABCD$
Theo định lý Pitago: \(AC=\sqrt{AB^2+BC^2}=\sqrt{10^2+10^2}=10\sqrt{2}\)
\(AH=\frac{1}{2}AC=5\sqrt{2}(dm)\)
Tiếp tục áp dụng định lý Pitago:
\(SH=\sqrt{SA^2-AH^2}=\sqrt{a^2-50}\)
Do đó \(V_{S.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{1}{3}.\sqrt{a^2-50}.100\)
Xét tam giác cân $SAB$ có đáy $AB=10$, hai cạnh $SA=SB=a$
Theo công thức Herong diện tích của tam giác là: \(\sqrt{p(p-a)(p-a)(p-10)}\) trong đó \(p=\frac{a+a+10}{2}=a+5\)
\(\Rightarrow S_{SAB}=5\sqrt{a^2-25}\)
\(\Rightarrow S_{xq}=20\sqrt{a^2-25}\)
Do \(V_{S.ABCD}=S_{xq}\Rightarrow \frac{100\sqrt{a^2-50}}{3}=20\sqrt{a^2-25}\)
Giải pt trên ta thu được \(a=\frac{5\sqrt{41}}{4}\) (dm)
Do đó:
Chiều cao hình chóp: \(SH=\sqrt{a^2-50}=\frac{15}{4}\) (dm)
\(S_{xq}=V=20\sqrt{a^2-25}=125\)