
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

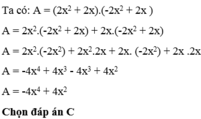

a)
2x-4=2(x-2)
2x+4=2(x+2)
x
Để P xác định thì
[2(x-2) => [2(x+2)
[2(x+2) =>[ 2(x-2)
[ (x-2)(x+2) => [(x+2)(x-2)
Vay 2(x+2) , 2(x-2), (x+2)(x-2) thi P xác định

Lời giải:
ĐK:.....
\(P=\left[\frac{x^2-2x+4}{x-2}.\frac{1}{x^3+8}+\frac{x-2}{x^3+8}.\frac{x^2-2x+4}{x^2-4}\right].(x^2-4)\)
\(P=\left[\frac{x^2-2x+4}{x-2}.\frac{1}{(x+2)(x^2-2x+4)}+\frac{x-2}{(x+2)(x^2-2x+4)}.\frac{x^2-2x+4}{(x-2)(x+2)}\right](x^2-4)\)
\(P=\left[\frac{1}{(x-2)(x+2)}+\frac{1}{(x+2)^2}\right](x^2-4)\)
\(=1+\frac{x^2-4}{(x+2)^2}=1+\frac{x-2}{x+2}=\frac{2x}{x+2}\)
b) Với \(x=-\frac{1}{2}\Rightarrow P=\frac{-2}{3}\)

a, \(\frac{x^{32}+x^{16}+1}{x^{16}+x^8+1}\)
\(=\frac{x^8+x^4+1}{x^4+x^2+1}\) Vậy phân thức \(a=\frac{x^8+x^4+1}{x^4+x^2+1}\)
P/s; Căn thức a, là phân số tối giản
b, \(\frac{x^8+3x^4+4}{x^4+x^2+2}\)
\(=\frac{x^4+3x^2+2}{x^2+x^1+1}\) Vậy căn thức \(b=\frac{x^4+3x^2+2}{x^2+x^1+1}\)
P/s; Căn thức b, có thể rút gọn được cho 2 và 4
Em ko chắc đâu nhé *-*

b) \(\frac{x^4-5x^2+4}{x^4-x^2+4x-4}\)
\(=\frac{x^4-x^2-4x^2+4}{x^2\left(x^2-1\right)+4\left(x-1\right)}\)
\(=\frac{\left(x^2-1\right)\left(x^2-4\right)}{\left(x-1\right)\left(x^3+x^2+4\right)}\)
\(=\frac{\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)}{\left(x-1\right)\left(x^3+x^2+4\right)}\)
\(=\frac{\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)}{\left(x-1\right)\left(x+2\right)\left(x^2-x+2\right)}\)
\(=\frac{x^2-x-2}{x^2-x+2}\)

=\(\frac{x}{x+2}.\frac{x+2}{4}-\frac{\left(x-2\right)\left(x^2+2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}.\frac{x^2-2x+4}{\left(x-2\right)\left(x+2\right)}.\frac{x+2}{4}=\frac{x}{4}+\frac{x^2+2x+4}{4\left(x+2\right)}=\frac{x^2+2x+x^2+2x+4}{4\left(x+2\right)}=\frac{x^2+\left(x+2\right)^2}{4\left(x+2\right)}\)Có j ko biết thì hỏi nha...Chúc học dốt.....Dỏi thơn