Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) \(A=\dfrac{3x+15}{x^2-9}+\dfrac{1}{x+3}-\dfrac{2}{x-3}\)
\(A=3x+15+x-3-2\left(x+3\right)\)
\(A=4x+10-2x-6\)
\(A=2x+4\)
b ) Để \(A=\dfrac{1}{2}\) thì \(2x+4=\dfrac{1}{2}\), ta có :
\(2x+4=\dfrac{1}{2}\)
\(\Leftrightarrow2x=\dfrac{1}{2}-4\)
\(\Leftrightarrow2x=\dfrac{-7}{2}\)
\(\Leftrightarrow x=\dfrac{-7}{4}\)
Vậy để \(A=\dfrac{1}{2}\) thì \(x=\dfrac{-7}{4}\)

Lời giải:
ĐKXĐ: \(x\neq \left\{2;\pm 3\right\}\)
a) Ta có:
\(P=\left(\frac{x^2-3x}{x^2-9}-1\right):\left(\frac{9-x^2}{x^2+x-6}-\frac{x-3}{2-x}-\frac{x-2}{x+3}\right)\)
\(P=\left(\frac{x(x-3)}{(x-3)(x+3)}-1\right):\left(\frac{(3-x)(3+x)}{(x-2)(x+3)}-\frac{3-x}{x-2}-\frac{x-2}{x+3}\right)\)
\(P=\left(\frac{x}{x+3}-1\right):\left(\frac{3-x}{x-2}-\frac{3-x}{x-2}-\frac{x-2}{x+3}\right)\)
\(P=\frac{x-(x+3)}{x+3}:\left(-\frac{x-2}{x+3}\right)=\frac{-3}{x+3}.\frac{x+3}{-(x-2)}=\frac{3}{x-2}\)
b) \(x^3-3x+2=0\)
\(\Leftrightarrow (x^3-x)-2(x-1)=0\)
\(\Leftrightarrow x(x-1)(x+1)-2(x-1)=0\)
\(\Leftrightarrow (x-1)(x^2+x-2)=0\)
\(\Leftrightarrow (x-1)[(x^2-1)+(x-1)]=0\)
\(\Leftrightarrow (x-1)^2(x+2)=0\) \(\Leftrightarrow \left[\begin{matrix} x=1\\ x=-2\end{matrix}\right.\)
Với \(x=1\Rightarrow P=\frac{3}{1-2}=-3\)
Với \(x=-2\Rightarrow P=\frac{3}{-2-2}=\frac{-3}{4}\)
c)
\(P=\frac{3}{x-2}\in\mathbb{Z}\Leftrightarrow 3\vdots x-2\)
\(\Leftrightarrow x-2\in \text{Ư}(3)\Rightarrow x-2\in\left\{\pm 1; \pm 3\right\}\)
\(\Leftrightarrow x\in \left\{3,1,5,-1\right\}\)
Do \(x\neq 3\Rightarrow x\in \left\{-1,1,5\right\}\)

\(\left(\dfrac{9}{x^3-9x}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x^2+3x}-\dfrac{x}{x^2-9}\right)\)
\(=\left(\dfrac{9}{x\left(x-3\right)\left(x+3\right)}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x\left(x+3\right)}-\dfrac{x}{\left(x-3\right)\left(x+3\right)}\right)\)
\(=\dfrac{9+x^2-3x}{x\left(x-3\right)\left(x+3\right)}:\dfrac{x^2-6x+9-x^2}{x\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-3x+9}{-6x+9}\)

a) Rút gọn :
P = \(\left(\dfrac{2x}{x+3}+\dfrac{10}{x-3}-\dfrac{2x^2+14}{x^2-9}\right):\dfrac{4}{x+3}\)
\(ĐKXĐ:\left\{{}\begin{matrix}x+3\ne0\\x-3\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne-3\\x\ne3\end{matrix}\right.\)
Ta có : \(P=\left[\dfrac{2x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}+\dfrac{10\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{2x^2+14}{\left(x+3\right)\left(x-3\right)}\right].\dfrac{x+3}{4}\)
\(P=\dfrac{2x^2-6x+10x+30-2x^2-14}{\left(x+3\right)\left(x-3\right)}.\dfrac{x+3}{4}\)
\(P=\dfrac{4x+16}{4x-13}=\dfrac{x+4}{x-3}\)
b) |x| = 3 => \(\left\{{}\begin{matrix}\left|x\right|=3khix\ge0\\\left|x\right|=-3khix< 0\end{matrix}\right.\)
* TH1 : x \(\ge0\)
\(P=\dfrac{x+4}{x-3}=\dfrac{3+4}{3-3}\left(koTMvìmẫu\ne0\right)\)
* TH2 : x < 0
\(P=\dfrac{x+4}{x-3}=\dfrac{-3+4}{-3-3}=\dfrac{-1}{6}\left(Tm\right)\)
c) Để P = \(\dfrac{-1}{2}\) thì :
\(\dfrac{x+4}{x-3}=\dfrac{-1}{2}\)
\(\Leftrightarrow2x+8=3-x\)
\(\Leftrightarrow2x+x=-8+3\)
\(\Leftrightarrow3x=-5\Rightarrow x=\dfrac{-5}{3}\)
d) P \(\le\) 2
<=> \(\dfrac{x+4}{x-3}\le2\)
\(\Leftrightarrow\dfrac{x+4}{x-3}-\dfrac{2x-6}{x-3}\le0\)
\(\Leftrightarrow\dfrac{10-x}{x-3}\le0\)
Lập bang xét dấu và tìm x nhé!!

a) \(\dfrac{x+1}{2}+\dfrac{3x-2}{3}=\dfrac{x-7}{12}\)
\(\Leftrightarrow\dfrac{6\left(x+1\right)+4\left(3x-2\right)}{12}=\dfrac{x-7}{12}\)
\(\Leftrightarrow6\left(x+1\right)+4\left(3x-2\right)=x-7\)
\(\Leftrightarrow6x+6+12x-8=x-7\)
\(\Leftrightarrow6x+12x-x=-7-6+8\)
\(\Leftrightarrow17x=-5\)
\(\Leftrightarrow x=\dfrac{-5}{17}\)
Vậy .........................
b) \(\dfrac{2x}{x-3}-\dfrac{5}{x+3}=\dfrac{x^2+21}{x^2-9}\left(ĐKXĐ:x\ne\pm3\right)\)
\(\Leftrightarrow\dfrac{2x\left(x+3\right)-5\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{x^2+21}{\left(x-3\right)\left(x+3\right)}\)
\(\Rightarrow2x\left(x+3\right)-5\left(x-3\right)=x^2+21\)
\(\Leftrightarrow2x^2+6x-5x+15=x^2+21\)
\(\Leftrightarrow2x^2-x^2+x+15-21=0\)
\(\Leftrightarrow x^2+x-6=0\)
\(\Leftrightarrow x^2-2x+3x-6=0\)
\(\Leftrightarrow x\left(x-2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(n\right)\\x=-3\left(l\right)\end{matrix}\right.\)
Vậy \(S=\left\{2\right\}\)
d) \(\left(x-4\right)\left(7x-3\right)-x^2+16=0\)
\(\Leftrightarrow\left(x-4\right)\left(7x-3\right)-\left(x^2-16\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(7x-3\right)-\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(7x-3-x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(6x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\6x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{7}{6}\end{matrix}\right.\)
Vậy .........................
P/s: các câu còn lại tương tự, bn tự giải nha

Bài 1:
a: \(A=\dfrac{x^4+x^3+x+1}{x^4-x^3+2x^2-x+1}=\dfrac{x^3\left(x+1\right)+\left(x+1\right)}{x^4-x^3+x^2+x^2-x+1}\)
\(=\dfrac{\left(x+1\right)\left(x^3+1\right)}{\left(x^2-x+1\right)\left(x^2+1\right)}=\dfrac{\left(x+1\right)^2}{x^2+1}\)
Để A=0 thì x+1=0
hay x=-1
b: \(B=\dfrac{x^4-5x^2+4}{x^4-10x^2+9}=\dfrac{\left(x^2-1\right)\left(x^2-4\right)}{\left(x^2-1\right)\left(x^2-9\right)}=\dfrac{x^2-4}{x^2-9}\)
Để B=0 thi (x-2)(x+2)=0
=>x=2 hoặc x=-2

Sửa đề:
\(Q=1+\left(\dfrac{x+1}{x^3+1}-\dfrac{1}{x^2-x+1}-\dfrac{2}{x+1}\right):\dfrac{x^3-2x^2}{x^3-x^2+x}\)
\(=1+\left(\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}-\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}-\dfrac{2\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\right):\dfrac{x^2\left(x-2\right)}{x\left(x^2-x+1\right)}\)
\(=1+\dfrac{x+1-x-1-2x^2+2x-2}{\left(x+1\right)\left(x^2-x+1\right)}:\dfrac{x^2\left(x-2\right)}{x\left(x^2-x+1\right)}\)
\(=1+\dfrac{-2x^2+2x-2}{\left(x+1\right)\left(x^2-x+1\right)}:\dfrac{x\left(x-2\right)}{x^2-x+1}\)
\(=1+\dfrac{-2\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\cdot\dfrac{x^2-x+1}{x\left(x-2\right)}\)
\(=1+\dfrac{-2\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-2x\right)}=\dfrac{\left(x+1\right)\left(x^2-2x\right)-2\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-2x\right)}\)
\(=\dfrac{x^3-2x^2+x^2-2x-2x^2+2x-2}{\left(x+1\right)\left(x^2-2x\right)}\)
\(=\dfrac{x^3-3x^2-2}{\left(x+1\right)\left(x^2-2x\right)}\)

a. \(\Leftrightarrow\dfrac{x+2}{98}+1+\dfrac{x+4}{96}+1=\dfrac{x+6}{94}+1+\dfrac{x+8}{92}+1\)
\(\Leftrightarrow\dfrac{x+100}{98}+\dfrac{x+100}{96}=\dfrac{x+100}{94}+\dfrac{x+100}{92}\)
\(\Leftrightarrow\left(x+100\right)\left(\dfrac{1}{98}+\dfrac{1}{96}-\dfrac{1}{94}-\dfrac{1}{92}\right)=0\)
\(\Leftrightarrow x+100=0\Leftrightarrow x=-100\)
c. \(\Leftrightarrow3x^2+3x-x-1=0\Leftrightarrow3x\left(x+1\right)-\left(x+1\right)=0\Leftrightarrow\left(x+1\right)\left(3x-1\right)=0\Leftrightarrow\left[\begin{matrix}x+1=0\\3x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[\begin{matrix}x=-1\\x=\dfrac{1}{3}\end{matrix}\right.\)
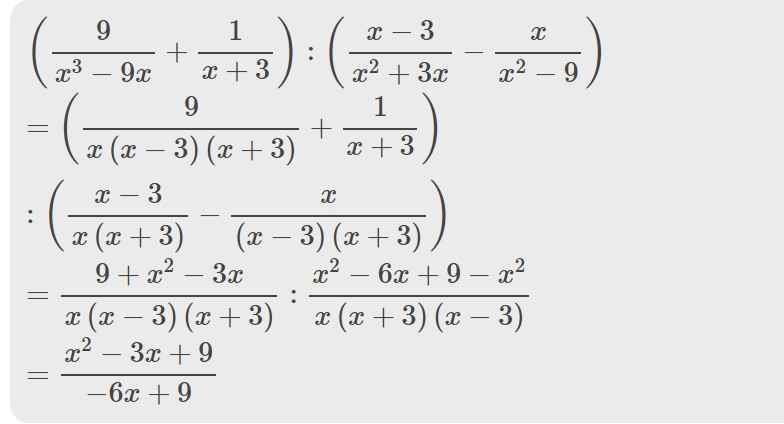

\(B=\dfrac{x^2+39}{\left(x-3\right)\left(x+3\right)}+\dfrac{8}{x+3}-\dfrac{1}{x-3}\)
\(=\dfrac{x^2+39+8x-24-x-3}{\left(x-3\right)\left(x+3\right)}=\dfrac{x^2+7x+12}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{\left(x+3\right)\left(x+4\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{x+4}{x-3}\)
\(B=\dfrac{x^2+39}{x^2-9}+\dfrac{8}{x+3}+\dfrac{1}{3-x}\) (ĐK: \(x\ne3,x\ne-3\))
\(B=\dfrac{x^2+39}{\left(x+3\right)\left(x-3\right)}+\dfrac{8\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{1}{x-3}\)
\(B=\dfrac{x^2+39+8x-24}{\left(x+3\right)\left(x-3\right)}-\dfrac{1}{x-3}\)
\(B=\dfrac{x^2+8x+15}{\left(x+3\right)\left(x-3\right)}-\dfrac{x+3}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x^2+8x+15-x-3}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x^2+7x+12}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{\left(x+3\right)\left(x+4\right)}{\left(x-3\right)\left(x+3\right)}\)
\(B=\dfrac{x+4}{x-3}\)