K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BT
0
HV
Rút gọn biểu thức
A=Căn ((2 căn 10 + căn 30 - 2 căn 2 - căn 6)/(2 căn 10 - 2 căn 2)) ÷ 2/ ( căn 3 -1)
0
15 tháng 8 2021
có bộ gõ kí hiệu Toán mà :))
ĐK : a >= 0 ; a khác 36
\(K=\left[\frac{a+14\sqrt{a}+100}{\left(\sqrt{a}-6\right)\left(\sqrt{a}+7\right)}+\frac{\left(\sqrt{a}+6\right)\left(\sqrt{a}-6\right)}{\left(\sqrt{a}-6\right)\left(\sqrt{a}+7\right)}-\frac{\left(\sqrt{a}-7\right)\left(\sqrt{a}+7\right)}{\left(\sqrt{a}-6\right)\left(\sqrt{a}+7\right)}\right]\div\left(\frac{\sqrt{a}-6}{\sqrt{a}-6}-\frac{\sqrt{a}-7}{\sqrt{a}-6}\right)\)
\(=\frac{a+14\sqrt{a}+100+a-36-a+49}{\left(\sqrt{a}-6\right)\left(\sqrt{a}+7\right)}\div\frac{1}{\sqrt{a}-6}\)
\(=\frac{a+14\sqrt{a}+113}{\left(\sqrt{a}-6\right)\left(\sqrt{a}+7\right)}\cdot\left(\sqrt{a}-6\right)=\frac{a+14\sqrt{a}+113}{\sqrt{a}+7}\)
Để K = 2 thì \(\frac{a+14\sqrt{a}+113}{\sqrt{a}+7}=2\Rightarrow a+14\sqrt{a}+113=2\sqrt{a}+14\Leftrightarrow a+12\sqrt{a}+99=0\)
Với a >= 0 thì \(a+12\sqrt{a}+99\ge99>0\)=> Không có giá trị x thỏa mãn K = 2
Ta có : \(K=\frac{a+14\sqrt{a}+113}{\sqrt{a}+7}=\frac{\left(a+14\sqrt{a}+49\right)+64}{\sqrt{a}+7}=\frac{\left(\sqrt{a}+7\right)^2+64}{\sqrt{a}+7}\)
\(=\left(\sqrt{a}+7\right)+\frac{64}{\sqrt{a}+7}\ge2\sqrt{\left(\sqrt{a}+7\right)\cdot\frac{64}{\sqrt{a}+7}}=16\)( bđt AM-GM )
Dấu "=" xảy ra <=> \(\sqrt{a}+7=\frac{64}{\sqrt{a}+7}\Rightarrow a=1\left(tm\right)\). Vậy MinK = 16
NA
2
5 tháng 7 2016
Ý bạn là thế này : \(\sqrt{27+12\sqrt{2}}\)Không rút gọn được bạn nhé ^^
Gợi ý cho bạn : \(\sqrt{17+12\sqrt{2}}=\sqrt{\left(2\sqrt{2}+3\right)^2}=2\sqrt{2}+3\)
NN
5 tháng 7 2016
Mk ko hiểu bn ghi đề bài gì cả sao lại căn bậc hai của 27+ 12 căn bậc hai của 2 hai căn gần nhau à
HV
9 tháng 9 2021
\(\sqrt{11+6\sqrt{2}}=\sqrt{\left(3+\sqrt{2}\right)^2}=3+\sqrt{2}\)
23 tháng 6 2019
\(a,\)\(đkxđ\Leftrightarrow x\ge0\)và \(x-9\ne0\Rightarrow x\ne9\)
\(A=\frac{6\sqrt{x}}{x-9}-\frac{5\sqrt{x}}{3-\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+3}\)
\(\)\(=\frac{6\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\frac{5\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\frac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{6\sqrt{x}+5x+15\sqrt{x}+x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{18\sqrt{x}+6x}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{6\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\frac{6\sqrt{x}}{\sqrt{x}-3}\)
23 tháng 6 2019
\(b,\)Để \(A>2\)\(\Rightarrow\frac{6\sqrt{x}}{\sqrt{x}-3}>2\)
\(\Rightarrow\frac{6\sqrt{x}}{\sqrt{x}-3}>\frac{12\sqrt{x}}{x-3}\)
\(\Rightarrow\frac{6\sqrt{x}-12\sqrt{x}}{\sqrt{x}-3}>0\)
\(\Rightarrow\frac{6\sqrt{x}}{\sqrt{x}-3}< 0\)
Vì \(\sqrt{x}\ge0;\)\(6>0\)\(\Rightarrow6\sqrt{x}\ge0\)
\(\Rightarrow\frac{6\sqrt{x}}{\sqrt{x}-3}>0\Leftrightarrow\sqrt{x}-3< 0\)
\(\Rightarrow\sqrt{x}< 3\Rightarrow\sqrt{x}< \sqrt{9}\)\(\Leftrightarrow x< 9\)
Mà \(x\ge0\left(đkxđ\right)\)\(\Rightarrow0\le x< 9\)
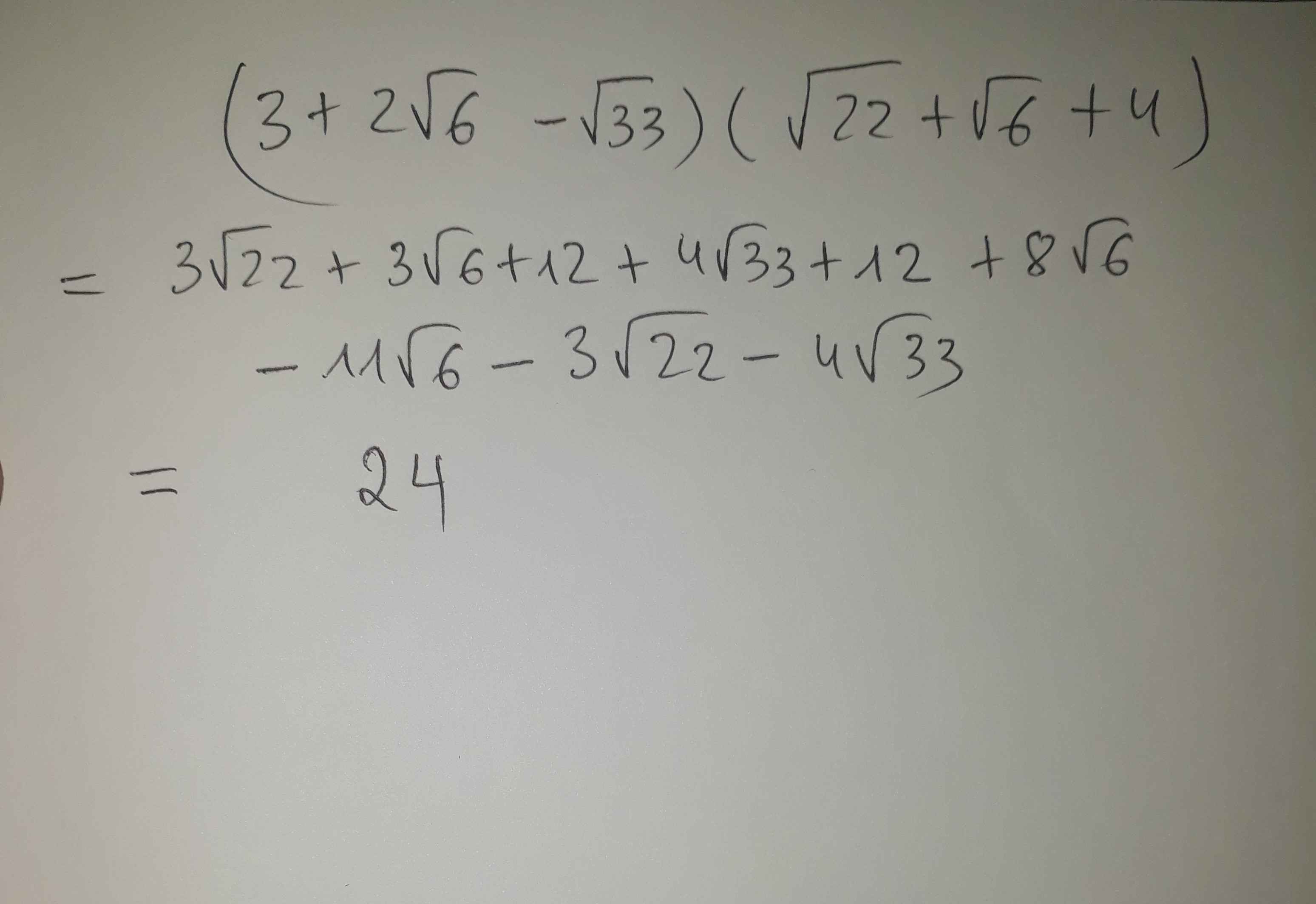
\(6\sqrt{6}-27=\left(\sqrt{6}-3\right)\left(9+3\sqrt{6}\right)\)