Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vật chuyển động từ trạng thái nghỉ đến vận tốc cực đại \(v_0\)
áp dụng công thức của chuyển động biến đổi đều ta có
\(2a_1s_1=v^2_0\)
Trong quá trình giảm dần đều ta cũng có
\(2a_2s_2=v^2_0\)
Theo đầu bài cho \(s_2=2s_1\) dẫn đến \(a_1=2a_2\)
Và thời gian \(\Delta t_2=2\Delta t_1\)

Chọn đáp án A
v = v 0 + a t → v 0 = 0 v = a t ⇒ a = v t = − 36. 1 3.6 ( m / s ) 10 = − 1 m / s

Chọn đáp án B
Đổi đơn vị v 0 = 36 k m / h = 10 m / s v = 54 k m / h = 15 m / s (Chú ý: 1 k m / h = 10 3 60.60 m / s = 1 3 , 6 m / s )
v 2 − v 0 2 = 2 a . s ⇒ a = v 2 − v 0 2 2 s = 15 2 − 10 2 2.625 = 0 , 1 m / s 2

Gọi khoảng cách giữa hai bến sông là S = AB, giả sử nước chảy từ A đến B với vận tốc u ( u < 3km/h )
- Thời gian thuyền chuyển động từ A đến B là: t1 = \(\frac{S}{v_1+u}\)
- Thời gian chuyển động của ca nô là: t2 = \(\frac{2S}{v_2-u}+\frac{2S}{v_2+u}\)
Theo bài ra: t1 = t2 \(\Leftrightarrow\frac{S}{v_1+u}=\frac{2S}{v_2-u}+\frac{2S}{v_2+u}\)
Hay: \(\frac{1}{v_1+u}=\frac{2}{v_2-u}+\frac{2}{v_2+u}\Rightarrow\)\(u^2+4v_2u+4v_1v_2-v^2_2=0\) \(\left(1\right)\)
Giải phương trình (1) ta được: \(u\approx\text{ - 0,506 km/h }\)
Vậy nước sông chảy theo hướng BA với vận tốc gần bằng 0,506 km/h
b. Nếu nước chảy nhanh hơn thì thời gian ca nô đi về về B (với quãng đường như câu a) có thay đổi không? vì sao?

Chọn B
Áp dụng định luật bảo toàn và chuyển hóa cơ năng ở hai vị trí chân dốc và ở vị trí đầu dốc
E 1 − E 0 = μ 1 m g S 1 → S t = 0 1 2 m v 0 2 ⏟ E 0 = 1 2 m v 2 + m g h ⏟ E 1 ⇒ v = v 0 2 − 2 g h
Áp dụng định luật bảo toàn và chuyển hóa cơ năng ở hai vị trí đầu dốc và vị trí vật dừng lại
0 − 1 2 m v 2 = − μ 2 m g . S 2 ⇒ S 2 = v 2 2 μ g = v 0 2 − 2 g h 2 μ g = 4 m

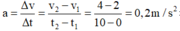
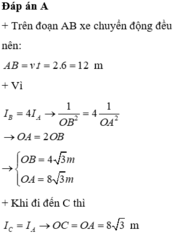
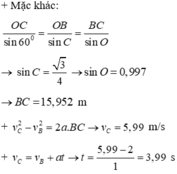
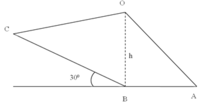
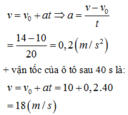

Chọn đáp án C