Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng kết quả bài 34 ta có:
+ MT2 = MA.MB
MA = 40m = 0,04km ;
MB = MA + AB = MA + 2R = 12800,04 km.
⇒ MT ≈ 22,63 km
+ M’T2 = M’A’.M’B’
M’A’ = 10m = 0,01km ;
M’B’ = M’A’ + A’B’ = M’A’ + 2R = 12800,01 km
⇒ M’T ≈ 11,31 km
⇒ MM’ = MT + M’T = 33,94 ≈ 34 km .
Vậy khi cách ngọn hải đăng khoảng 34km thì người thủy thủ bắt đầu trông thấy ngọn hải đăng.

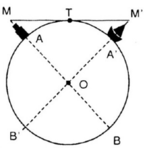
Áp dụng kết quả bài 34 ta có:
+ M T 2 = M A . M B
MA = 40m = 0,04km ;
MB = MA + AB = MA + 2R = 12800,04 km.
⇒ MT ≈ 22,63 km
+ M ’ T 2 = M ’ A ’ . M ’ B ’
M’A’ = 10m = 0,01km ;
M’B’ = M’A’ + A’B’ = M’A’ + 2R = 12800,01 km
⇒ M’T ≈ 11,31 km
⇒ MM’ = MT + M’T = 33,94 ≈ 34 km .
Vậy khi cách ngọn hải đăng khoảng 34km thì người thủy thủ bắt đầu trông thấy ngọn hải đăng.

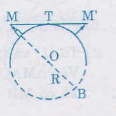
Áp dụng kết quả bài tập 34 ta có:
MT2 = MA. MB
MT2 = MA.(MA + 2R)
Thay số vào đẳng thức trên và lấy đơn vị là km, ta có:
MT2 = 0,04 (0,04 + 12.800)
MT ≈ 23 (km)
Cũng tương ta có;
MT2 = 0,01(0,01 +12.800)
MT ≈ 11 (km)
Từ đó: MM' = MT + M'T = 23+11= 34(km)
Vậy khi ngọn hải đăng khoảng 34 km thì người thủy thủ bắt đầu trông thấy ngọn hải đăng.

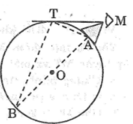
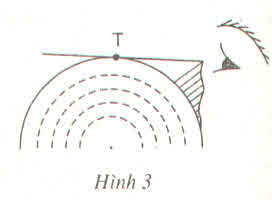
Điểm nhìn tối đa T là tiếp điểm của tiếp tuyến kẻ từ mắt đến bề mặt Trái Đất (như hình vẽ)
Xét hai tam giác MTA và MBT,ta có:
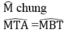
(hệ quả góc giữa tiếp tuyến và dây cung)
Suy ra ∆ MTA đồng dạng ∆ MBT
⇒ MT/MA = MB/MT => M T 2 = MA.MB
= MA (MA + 2R)
MA là chiều cao của đỉnh núi bằng 1km
Thay số ta có: M T 2 =1.(1 + 2.6400)=12801
Suy ra : MT ≈ 113,1(km)

chiếc thuyền đang đúng cách chân hải đăng \(\approx\)63,40m![]()

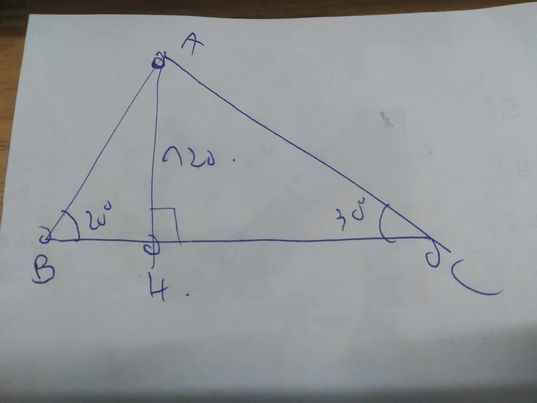
Gọi AH là độ cao của ngọn hải đăng, BC là độ dài quãng đường con thuyền đi được giữa hai lần quan sát.
Theo đề, ta có: AH=120m; \(\widehat{B}=20^0;\widehat{C}=30^0\)
Xét ΔAHB vuông tại H có \(tanB=\dfrac{AH}{HB}\)
=>\(HB=\dfrac{120}{tan20}\simeq329,7\left(m\right)\)
Xét ΔAHC vuông tại H có \(tanC=\dfrac{AH}{HC}\)
=>\(\dfrac{120}{HC}=tan30\)
=>\(HC=\dfrac{120}{tan30}\simeq207,85\left(m\right)\)
BC=BH+CH=329,7+207,85=537,55(m)
Vậy: Con thuyền đã được 537,55m giữa hai lần quan sát