K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HK
18 tháng 2 2020
Động lượng được bảo toàn:
\(m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}=m_1\overrightarrow{v_1'}+m_2\overrightarrow{v_2'}\)
\(\Leftrightarrow m_1v_1'-m_2v_2'=0\)
\(\Leftrightarrow\left(4000-10\right)v_1'=10.400\)
\(\Leftrightarrow v_1'\approx1\left(m/s\right)\)
17 tháng 1 2022
Chọn chiều dương là chiều chuyển động của viên đạn
ÁP dụng định luật bảo toàn động lượng ta có:
\(m_2v_2cos60-m_1v_1=0=>v_2=\dfrac{m_1v_1}{m_2cos60}=\dfrac{7500.1}{20.cos60}=750(m/s)\)
=> Chọn B
24 tháng 2 2022
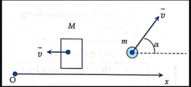
Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{0}\)
\(\Rightarrow p_2\cdot cos\alpha-p_1=0\)
\(\Rightarrow m_2\cdot v_2\cdot cos\alpha-m_1\cdot v_1=0\)
\(\Rightarrow v_2=\dfrac{m_1\cdot v_1}{m_2\cdot cos\alpha}=\dfrac{8000\cdot500}{2\cdot cos60^o}=4\cdot10^6\)m/s
HQ
21 tháng 2 2021
Phương trình bảo toàn vecto động lượng cho hệ theo Ox ( Vì theo Ox khi hợp lực tác dụng vào vật theo phương Ox bị triệt tiêu ) O---------->x
\(\overrightarrow{0}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
Vì trước khi bắn hệ đứng yên: Chiếu phương trình lên trục Ox ta được: \(0=-p_1+p_2\cos\left(60^0\right)\) Thay số:
\(0=-m_1v_1+m_2v_2\cos\left(60^0\right)\Rightarrow v_2=\dfrac{m_1v_1}{m_2\cos\left(60^0\right)}\) Thay số nốt hộ mình là ra :D
23 tháng 2 2022
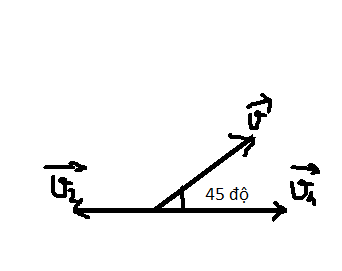
Chọn chiều dương là chiều nòng súng hướng phía trc.
Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
\(\Rightarrow m_1\cdot v_1\cdot cos45^o+m_2\cdot v_2=0\)
\(\Rightarrow4000\cdot v_1\cdot cos45^o+10\cdot500=0\)
\(\Rightarrow v_1\approx1,77\)m/s
1 tháng 3 2022
Câu 1.
Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
\(\Rightarrow m_1\cdot v_1+m_2\cdot v_2=\left(m_1+m_2\right)\cdot V\)
\(\Rightarrow2000\cdot30+3000\cdot40=\left(2000+3000\right)\cdot V\)
\(\Rightarrow V=36\)m/s
Câu 2.
Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{0}\)
\(\Rightarrow-p_1+p_2=0\)
\(\Rightarrow p_1=p_2\Rightarrow m_1\cdot v_1=m_2\cdot v_2\)
\(\Rightarrow7500\cdot1=20\cdot v_2\)
\(\Rightarrow v_2=375\)m/s
3 tháng 5 2016
Công để nâng khối đá thứ hai chồng lên khối đá thứ nhất:
A1=PhA1=Ph, với P là trọng lượng của một khối đá và h là chiều cao của một khối đá.
Công để nâng khối đá thứ ba chồng lên khối đá thứ hai:
A2=P.2hA2=P.2h
Công để nâng khối đá thứ mười hai chồng lên khối đá thứ mười một:
A12=P.11hA12=P.11h
Tổng công cần thiết là:
A=A1+A2+...+A12=P(h+2h+...+11h)A=A1+A2+...+A12=P(h+2h+...+11h)
=mgh(1+2+...+11)=mgh(1+2+...+11)
Trong ngoặc đơn là tổng các số tự nhiên từ 1 đến 11, có giá trị là:
11(11+1)2=6611(11+1)2=66
Do đó: A=66mgh=26400JA=66mgh=26400J.
10 tháng 2 2020
\(m_1=500kg\)
\(m_2=5kg\)
\(v_2=5m/s\)
v1 =?
Theo định luật bảo toàn động lượng ta có :
\(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{0}\)
=> p1 =p2
<=> \(m_1v_1=m_2v_2\)
=> \(v_1=\frac{m_2v_2}{m_1}=\frac{5.5}{500}=0,05\left(m/s\right)\)
mình gửi nhầm đầu bài ạ