Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc cano lúc nước yên lặng là x
Độ dài AB lúc đi là 2(x+5)
Độ dài AB lúc về là 2,5(x-5)
Theo đề, ta có: 2,5(x-5)=2(x+5)
=>2,5x-12,5=2x+10
=>0,5x=22,5
=>x=45

Gọi vận tốc thực của ca nô là x ( km/h ) ( đk : x > 2 )
\(\Rightarrow\)Vận tốc của ca nô khi xuôi dong là : x + 2 ( km/h)
\(\Rightarrow\)khúc sông AB dài : 4 ( x + 2 ) (km)
\(\Rightarrow\)Vận tốc của ca nô khi ngược dòng là : x - 2 (km/h)
\(\Rightarrow\)Khúc sông AB dài : 5 ( x - 2 ) (km)
Vì khúc sông AB có độ dài không đổi nên ta có pt :
4 ( x + 2 ) = 5 ( x - 2 ) (1)
Giải pt (1) ta có :
pt (1) \(\Leftrightarrow\)4x + 8 = 5x -10
\(\Rightarrow\)x = 18 ( tm)
Vậy vận tốc thực của ca nô là 18 km/h

Gọi khoảng cách giữa hai bến A và B là x ( km), ĐK: x > 0 .
Khi đó: Vận tốc của ca nô đi từ A đến B là : x5x5(km/h)
Vận tốc của ca nô đi từ B đến A là : x7x7 (km/h)
Theo đề ra ta có phương trình: 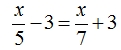
Giải phương trình và đến kết quả x = 105 ( thoả mãn)
Vậy khoảng cách giữa hai bến A và B là 105 km.
gọi vận tốc của tàu là v. (v>3)
khi đó vận tốc thực của tàu khi đi từ a đến b là v+3(km)
suy ra AB=5x(v+3) (1)
vận tốc thực của tàu khi đi từ b về a là v-3 (km)
suy ra AB=7x(v-3) (2)
từ (1) (2) có: v=18 km (tm)

Gọi quãng đường AB là l
vận tốc của ca nô là : \(V_c\)
vận tốc của dòng nước là: \(V_n\)
*) Khi ca nô đi xuôi dòng từ A-> B thì \(l=4\left(V_c+V_n\right)\)
*) Khi ca nô đi ngược dòng từ A -> B thì \(l=5\left(V_c-V_n\right)\)
=> \(4\left(V_c+V_n\right)=5\left(V_c-V_n\right)=>4V_c+4V_n=5V_c-5V_n=>9V_n=V_c=>V_c=180km\)/h
=>l=5.160=800km.
Lời giải:
Đổi $2h30'=2,5$ h
Gọi vận tốc cano khi nước im lặng là $a$ km/h
Vận tốc ngược dòng: $a-5=\frac{BA}{2,5}$ (km/h)
Vận tốc xuôi dòng: $a+5=\frac{AB}{2}$ (km/h)
$\Rightarrow (a+5)-(a-5)=\frac{AB}{2}-\frac{AB}{2,5}$
$\Leftrightarrow 10=\frac{AB}{10}$
$\Leftrightarrow AB=100$ (km)
Vận tốc cano khi nước im lặng: $a=\frac{AB}{2}-5=\frac{100}{2}-5=45$ (km/h)