Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi phương trình chính tắc của parabol là: \({y^2} = 2px\left( {p > 0} \right)\)
Vì \(AB = 40cm\) và \(h = 30cm\) nên \(A\left( {30;20} \right)\)
Do \(A\left( {30;20} \right)\) thuộc parabol nên ta có: \({20^2} = 2p.30 \Rightarrow p = \frac{{20}}{3}\)
Vậy parabol có phương trình chính tắc là: \({y^2} = \frac{{40}}{3}x\)

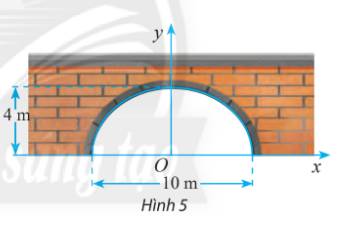
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)

Phương trình chính tắc của parabol (P) có dạng \({y^2} = 2px\left( {p > 0} \right)\).
a) Khi 1 đơn vị đo trong mặt phẳng tọa độ ứng với 1m trên thực tế, ta có \(B\left( {20;200} \right)\).
Thay tọa độ điểm B vào phương trình của (P) ta được \({200^2} = 2p.20 \Leftrightarrow p = 1000\).
Vậy phương trình chính tắc của (P) là: \({y^2} = 2000x\).
b) Khi 1 đơn vị đo trong mặt phẳng tọa độ ứng với 1km trên thực tế, ta có \(B\left( {0,02;0,2} \right)\).
Tương tự, ta có phương trình chính tắc của (P) là \({y^2} = 2x\).

Đáp án: B.
Ta có khoảng cách từ tiêu điểm đến đường chuẩn của một parabol bằng p ⇒ p = 2
Vậy phương trình chính tắc của parabol là: y 2 = 2.2x ⇔ y 2 = 4x

a) Tiêu điểm có tọa độ \((4;0)\) nên ta có \(p = 8\)
Suy ra phương trình chính tắc của parabol là: \({y^2} = 16x\)
b) Đường chuẩn có phương trình \(x = - \frac{1}{6}\), nên ta có \(p = - \frac{1}{3}\)
Suy ra phương trình chính tắc của parabol có dạng \({y^2} = - \frac{2}{3}x\)
c) Gọi phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Thay tọa độ điểm \((1;4)\) vào phương trình \({y^2} = 2px\) ta có:
\({4^2} = 2p.1 \Rightarrow p = 8\)
Vậy phương trình chính tắc của parabol là \({y^2} = 16x\)
d) Gọi \(F\left( {\frac{p}{2};0} \right)\), \(\Delta :x + \frac{p}{2} = 0\) lần lượt là tiêu điểm và phương trình đường chuẩn của parabol ta có:
\(d\left( {F,\Delta } \right) = \frac{{\left| {\frac{p}{2} + \frac{p}{2}} \right|}}{1} = 8 \Rightarrow p = 8\)
Vậy phương trình chính tắc của parabol là \({y^2} = 16x\)

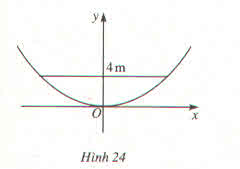
Pra bol đối xứng qua trục Tung => điểm cao nhất thuộc Parabol có tọa độ (2,h)
\(x=2\Rightarrow y=\dfrac{1}{2}\Rightarrow a.2^2=\dfrac{1}{2}\Rightarrow a=\dfrac{1}{8}\)

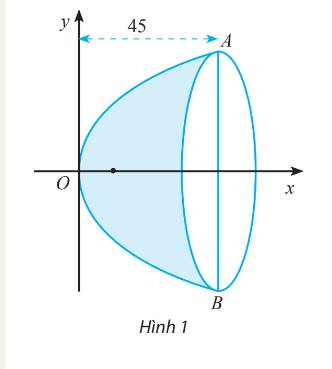
Từ giả thiết ta có tiêu điểm \(F(5;0)\), suy ra \(\frac{p}{2} = 5\) hay \(p=10\).
Vậy phương trình chính tắc của parabol là: \({y^2} = 20x\)
Chiều sâu của gương là 45 cm tương ứng với \({x_A} = 45\), thay \({x_A} = 45\) vào phương trình \({y^2} = 20x\) ta có: \({y^2} = 20.45 = 900 \Rightarrow {y_A} = 30 \Rightarrow AB = 2{y_A} = 60 \)
Vậy khoảng cách AB là \(60 cm\)
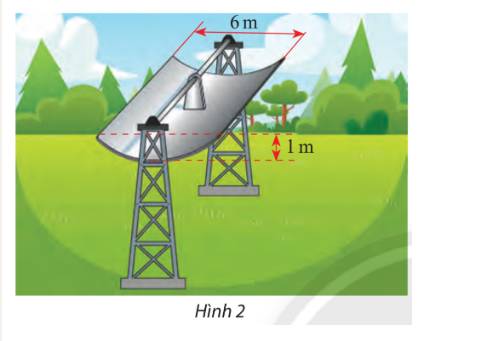
a) Vẽ lại parabol mô phỏng mặt cắt trên như hình dưới
Ta có: \(OA = 1,BC = 2{y_B} = 6 \Rightarrow B\left( {1;3} \right)\)
Giả sử phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Thay tọa độ điểm B vào phương trình \({y^2} = 2px\) ta có: \({3^2} = 2p.1 \Rightarrow p = \frac{9}{2}\)
Vậy phương trình chính tắc của parabol mô phỏng mặt cắt trên là \({y^2} = 9x\)
b) Khoảng cách từ tâm đường ống đến đỉnh của parabol chính là độ dài từ đỉnh tới tiêu điểm của parabol
Từ phương trình chính tắc ta có tiêu điểm \(F\left( {\frac{9}{4};0} \right)\)
Vậy khoảng cách từ tâm đường ống đến đỉnh của parabol là \(\frac{9}{4}\) m