Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
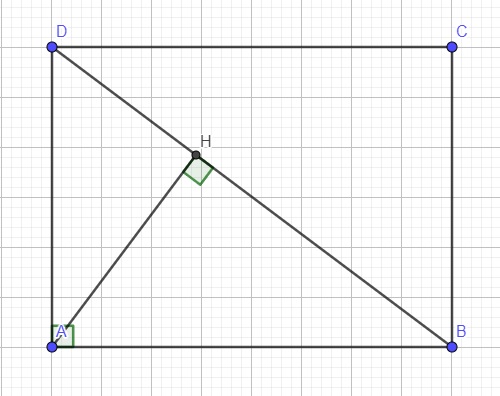
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)

Answer:
A C B N M P
Xét tam giác ABC:
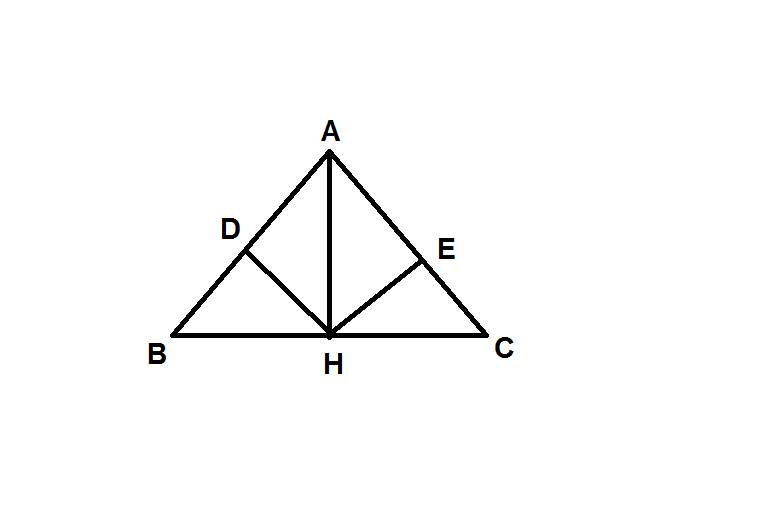
M, N, P lần lượt là trung điểm của AB, AC, BC
=> MN, MP, NP là đường trung bình của tam giác ABC
\(\Rightarrow\frac{MN}{BC}=\frac{MP}{AC}=\frac{NP}{AB}=\frac{1}{2}\)
Xét tam giác PMN và tam giác ACB
\(\frac{PM}{AC}=\frac{MN}{CB}=\frac{PN}{AB}=\frac{1}{2}\)
Vậy tam giác PMN đồng dạng với tam giác ACB

Câu 1 : Nếu 2 tam giác vuông có 2 góc nhọn tương ứng bằng nhau thì chúng được gọi là đồng dạng với nhau vì đương nhiên trừ góc vuông ở cả hai tam giác vuông thì góc nhọn còn lại đương nhiên phải bằng nhau.
Câu 2 : Nếu cạnh huyền và cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác đồng dạng. Nếu hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác đồng dạng.
Thật ra là bạn viết tam giác nào trước cũng được, nhưng phải đúng theo thứ tự tên góc, cạnh tương ứng
Mk cảm ơn :D