Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$1440=2^5.3^2.5$
Để $k=n!\vdots 1440$ thì $n!\vdots 2^5$; $n!\vdots 3^2; n!\vdots 5$
Để $n!\vdots 3^2; 5$ thì $n\geq 6(1)$
Để $n!\vdots 2^5$. Để ý $2=2^1, 4=2^2, 6=2.3, 8=2^3$. Để $n!\vdots 2^5$ thì $n\geq 8(2)$
Từ $(1); (2)$ suy ra $n\geq 8$. Giá tri nhỏ nhất của $n$ có thể là $8$

\(g\left(x\right)=x^4-4x^3+4x^2+a\)
\(g'\left(x\right)=4x^3-12x^2+8x=0\Leftrightarrow4x\left(x^2-3x+2\right)\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)
\(f\left(0\right)=f\left(2\right)=\left|a\right|\) ; \(f\left(1\right)=\left|a+1\right|\)
TH1: \(\left\{{}\begin{matrix}M=\left|a\right|\\m=\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a\right|\ge\left|a+1\right|\\\left|a\right|\le2\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{2}{3}\le a\le-\dfrac{1}{2}\\a\le-2\end{matrix}\right.\) \(\Rightarrow a=\left\{-3;-2\right\}\)
TH2: \(\left\{{}\begin{matrix}M=\left|a+1\right|\\m=\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a+1\right|\ge\left|a\right|\\\left|a+1\right|\le2\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-\dfrac{1}{2}\le a\le-\dfrac{1}{3}\\a\ge1\end{matrix}\right.\) \(\Rightarrow a=\left\{1;2;3\right\}\)

Chọn C
Gọi A (d; e; f) thì A thuộc mặt cầu (S1): (x - 1)2 + (y - 2)2 + (z- 3)2 = 1 có tâm I1 = (1; 2; 3), bán kính R1 = 1
B (a; b; c) thì B thuộc mặt cầu (S2): (x - 3)2 + (y - 2)2 + z2 = 9 có tâm I2 = (-3; 2; 0), bán kính R2 = 3
Ta có I1I2 = 5 > R1 + R2 => (S1) và (S2) không cắt nhau và ở ngoài nhau.
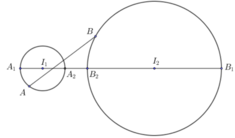
Dễ thấy F = AB, AB max khi A ≡ A1; B ≡ B1
=> Giá trị lớn nhất bằng I1I2 + R1 + R2 = 9.
AB min khi A ≡ A2; B ≡ B2
=> Giá trị nhỏ nhất bằng I1I2 - R1 - R2 = 1.
Vậy M - m =8

Lời giải:
Có \(f(x)=x-m^2+\frac{m}{x+1}\Rightarrow f'(x)=1-\frac{m}{(x+1)^2}\)
Do $m$ dương nên
\(f'(x)=0\Leftrightarrow (x+1)^2=m\Rightarrow x=\sqrt{m}-1\) hoặc \(x=-\sqrt{m}-1\) (TH này loại vì \(x\geq 0\))
Giờ ta chỉ cần thử giá trị của hàm tại những điểm đặc biệt thôi, vì giá trị cực trị bao giờ cũng xuất hiện ở những điểm đặc biệt của x
\(f(0)=-m^2+m=-2\Leftrightarrow m=2\)
\(f(1)=1-m^2+\frac{m}{2}=-2\Leftrightarrow m=2\)
\(f(\sqrt{m}-1)=\sqrt{m}-1-m^2+\frac{m}{\sqrt{m}-1}=-2\), em shift solve để giải thu được \(m=2,6.....\)
Đến đây theo thông thường ta phải thử lại giá trị của $m$ để tìm đáp án đúng nhất. Nhưng do chỉ tìm giá trị gần nhất thôi nên dễ thấy $m$ gần giá trị $3$ nhât, chọn đáp án B.

à:::::::::: a,b nguyên dương
\(S=8b^2+3b+8\)
vậy min S tại b=1 (số nguyên dương ) ......nhìn thôi cũng thấy rồi !
=>minS=19======>>>(B)
\(y'=\left(a-4\right)x^2+4bx+1\)
Để hàm số đồng biến trên R thì
\(\left\{{}\begin{matrix}a-4>0\\4b^2-\left(a-4\right)\le0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}a>4\\a-4\ge4b^2\end{matrix}\right.\)
ta thấy S=2a+3b nhỏ nhất khi a và b nhỏ nhất
ta thấy :\(a-4\ge4b^2\)
a và b sẽ mang giá trị nhỏ nhất khi \(a-4=4b^2\)
=>\(a=4b^2+4\)
vậy \(S=2\left(4b^2+4\right)+3b\)
vậy min S là : ...................
..............................
.................................
....................
\(-\infty\)
sao kì vậy ! may be lí luận sai chỗ nào đấy

Chọn A
Gọi (Q) là mặt phẳng đi qua M (2;2; -3) và song song với mặt phẳng (P).
Suy ra (Q):2x+y+z-3=0.
Do Δ // (P) nên Δ ⊂ (Q)).
D (N, Δ) đạt giá trị nhỏ nhất ó Δ đi qua N', với N' là hình chiếu của N lên (Q).
Gọi d là đường thẳng đi qua N và vuông góc (P), 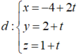
Ta có N’ ∈ d => N' (-4+2t;2+t;1+t); N’ ∈ (Q) => t = 4/3 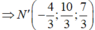
![]() cùng phương
cùng phương 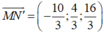
Do |a|, |b| nguyên tố cùng nhau nên chọn ![]()
Vậy |a| + |b| + |c| = 15.

+ Xét hàm số y= x4- 4x3+ 4x2+ a trên đoạn [ 0; 2].
Ta có đạo hàm y’ = 4x3-12x2+ 8x,
y
'
=
0
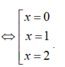
Khi đó; y( 0) = y( 2) = a; y( 1) = a+ 1
+ Nếu a≥ 0 thì M= a+ 1,m = a.
Để M ≤ 2m khi a≥ 1, suy ra a ∈ 1 ; 2 ; 3 thỏa mãn
+ Nếu a≤ - 1 thì M = a = - a , m = a + 1 = - a - 1 .
Để M≤ 2m thì a≤ -2, suy ra a a ∈ - 2 ; - 3
Vậy có 5 giá trị nguyên của a thỏa mãn yêu cầu.
Chọn B.


Chọn B