Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B. Điện trở của dây dẫn giảm đi 10 lần
Áp dụng công thức: 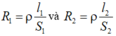
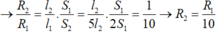

Ta có: \(R=\rho\cdot\dfrac{l}{S}\)
Nếu giảm \(l\) đi 3 lần, tăng S lên 2 lần thì điện trở của dây giảm 6 lần.

\(\dfrac{R_1}{R_2}=\dfrac{\rho\dfrac{l_1}{S_1}}{\rho\dfrac{l_2}{S_2}}=\dfrac{l_1}{S_1}.\dfrac{S_2}{l_2}=\dfrac{l_1}{S_1}.\dfrac{\dfrac{1}{2}S_1}{3l_1}=\dfrac{1}{6}\Rightarrow R_2=6R_1\)
Vậy điện trở của dây tăng gấp 6 lần

Ta có: 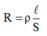
Nếu chiều dài dây dẫn giảm đi 5 lần và tiết diện tăng 2 lần thì điện trở của dây dẫn thay đổi: 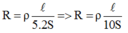
Điện trở của dây dẫn giảm đi 10 lần
→ Đáp án B

Ta có: 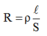
Nếu chiều dài dây dẫn giảm đi 5 lần và tiết diện tăng 2 lần thì điện trở của dây dẫn thay đổi: 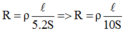
Điện trở của dây dẫn giảm đi 10 lần
→ Đáp án B

Theo đề bài, ta có: \(\left\{{}\begin{matrix}\rho=\rho'\\l=l'\\S'=2S\\R=?\end{matrix}\right.\)
Từ công thức \(R=\rho.\dfrac{l}{S}\rightarrow\rho=\dfrac{R.S}{l}\)
\(\rho=\rho'\\ \rightarrow\dfrac{R.S}{l}=\dfrac{R'.S'}{l}\\ \rightarrow R.S=R'.S'\\ \rightarrow R.S=R'.2S'\\ \rightarrow R=2.R'\\ \rightarrow R'=\dfrac{R}{2}\)
Vậy điện trở giảm 1 nửa
\(\rightarrow D\) Giảm đi 2 lần

Điện trở của dây được tính theo công thức: \(E=p.\dfrac{l}{S}\)
Với ℓ là chiều dài dây, S là tiết diện.
Khi tiết diện dây tăng lên 2 lần thì: \(R'=p.\dfrac{l}{2S}=\dfrac{R}{2}\)
\(R=\rho\dfrac{l}{S}\)
\(R'=\rho\dfrac{2l}{\dfrac{1}{2}S}=\rho\dfrac{4l}{S}=4R\)

l tăng 2 =) R tăng 2
S giảm 2 =) R tăng 2
=) R tăng 2.2=4 lần
Còn vì sao l tăng R tăng , S giảm R tăng thì có ở SGK rồi nhé