Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tại t = 0 vật ở vị trí x = + A
- Sau Δ t = T / 6 < T / 2 vật ở vị trí x = √ 3 / 2 cm
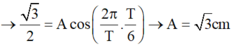

Để tính tốc độ trung bình của dao động trong thời gian 1818 chu kỳ, ta cần tính sự thay đổi li độ và thời gian tương ứng.
Theo phương trình dao động x = 2,5cos(10t), biết rằng biên độ A = 2,5 cm và chu kỳ T = 2π/10 = π/5.
Để tính sự thay đổi li độ, ta cần tính x(t) tại hai thời điểm khác nhau. Đầu tiên, ta tính x(t) tại thời điểm t = 0, khi vật có li độ x = 0:
x(0) = 2,5cos(10*0) = 2,5cos(0) = 2,5
Tiếp theo, ta tính x(t) tại thời điểm t = 1818T, khi đã qua 1818 chu kỳ:
x(1818T) = 2,5cos(10*1818T)
Sau đó, ta tính sự thay đổi li độ bằng cách lấy hiệu của hai giá trị li độ:
Δx = x(1818T) - x(0)
Để tính thời gian tương ứng, ta nhân số chu kỳ với 1818:
Δt = 1818T
Cuối cùng, ta tính tốc độ trung bình bằng cách chia sự thay đổi li độ cho thời gian tương ứng:
v(trung bình) = Δx/Δt
Với các giá trị đã tính được, ta có thể tính toán tốc độ trung bình của dao động trong thời gian 1818 chu kỳ

Chọn D

+ T = 2 π w = 2 π 2 π = 1 s
+ t = 0: x = 2cosπ = -2cm => chất điểm ở vị trí biên âm.
+ x = 3 cm = A 3 2
+ Sử vòng tròn: tmin = t-A→O + tO→ A 3 /2 = T 4 + T 6 = 5 T 12 = 5 12 s.
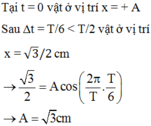

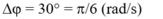
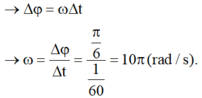
x = A.coswt đúng chưa
Sau t = T/8
x = A.cos(w.T/8) = A.cospi/4 = A/căn 2
mà x = 2 căn 2 cm
=> A/căn 2 = 2căn 2 => A = 4cm
Chú ý là w.T = 2pi nên w.T/8 = pi/4