
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\Rightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{5}{4}+\dfrac{2}{5}=\dfrac{3}{10}x-\dfrac{1}{4}x\)
\(\Rightarrow\dfrac{33}{20}=\dfrac{11}{20}x\)
\(\Rightarrow x=\dfrac{33}{20}\div\dfrac{11}{20}\)
\(\Rightarrow x=3\)
\(1\dfrac{1}{4}-x\dfrac{1}{4}=x\cdot30\%\cdot\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-x\dfrac{1}{4}=x\cdot\dfrac{3}{10}-\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Leftrightarrow25-5x=6x-8\)
\(\Leftrightarrow-5x-6x=-8-25\)
\(\Leftrightarrow-11x=-33\)
\(\Leftrightarrow x=3\)
Vậy x = 3

Theo mk được biết thì Shinichi và Kid là hai anh em nên mk thích cả hai



Trả lời:
\(\frac{5}{1.6}+\frac{5}{6.11}+...+\frac{5}{\left(5x+1\right)\left(5x+6\right)}=\frac{2005}{2006}\)
\(\Rightarrow1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+...+\frac{1}{5x+1}-\frac{1}{5x+6}=\frac{2005}{2006}\)
\(\Rightarrow1-\frac{1}{5x+6}=\frac{2005}{2006}\)
\(\Rightarrow\frac{1}{5x+6}=1-\frac{2005}{2006}\)
\(\Rightarrow\frac{1}{5x+6}=\frac{1}{2006}\)
\(\Rightarrow5x+6=2006\)
\(\Rightarrow5x=2000\)
\(\Rightarrow x=400\)
Vậy x = 400
Trả lời:
\(\frac{x}{2008}-\frac{1}{10}-\frac{1}{15}-\frac{1}{21}-...-\frac{1}{120}=\frac{5}{8}\)
\(\Rightarrow\frac{x}{2008}-\left(\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{120}\right)=\frac{5}{8}\)\(\frac{5}{8}\)
Đặt \(A=\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{120}\), ta được : \(\frac{x}{2008}-A=\frac{5}{8}\) (*)
\(\Rightarrow A=\frac{2}{20}+\frac{2}{30}+\frac{2}{42}+...+\frac{2}{240}\)
\(\Rightarrow A=2\left(\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+...+\frac{1}{240}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+...+\frac{1}{15.16}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{15}-\frac{1}{16}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4}-\frac{1}{16}\right)=2.\frac{3}{16}=\frac{3}{8}\)
Thay A vào (*) , ta có:
\(\frac{x}{2008}-\frac{3}{8}=\frac{5}{8}\)
\(\Rightarrow\frac{x}{2008}=1\)
\(\Rightarrow x=2008\)
Vậy x = 2008

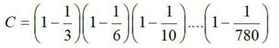



 Mình cảm ơn ạ
Mình cảm ơn ạ









\(C=\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{10}\right)...\left(1-\dfrac{1}{780}\right)\)
\(=\dfrac{2}{3}.\dfrac{5}{6}.\dfrac{9}{10}...\dfrac{779}{780}=\dfrac{2.2}{3.2}.\dfrac{5.2}{6.2}.\dfrac{9.2}{10.2}...\dfrac{779.2}{780.2}\)
\(=\dfrac{4}{6}.\dfrac{10}{12}.\dfrac{18}{20}...\dfrac{1558}{1560}=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}.\dfrac{3.6}{4.5}...\dfrac{38.41}{39.40}\)
\(=\dfrac{1.2.3...38}{2.3.4...39}.\dfrac{4.5.6...41}{3.4.5...40}=\dfrac{1}{39}.\dfrac{41}{3}=\dfrac{41}{117}\)
\(C=\left(1-\dfrac{2}{6}\right)\left(1-\dfrac{2}{12}\right)\left(1-\dfrac{2}{20}\right)...\left(1-\dfrac{2}{1560}\right)\)
\(=\left(1-\dfrac{2}{2.3}\right)\left(1-\dfrac{2}{3.4}\right)\left(1-\dfrac{2}{4.5}\right)...\left(1-\dfrac{2}{39.40}\right)\)
Ta có: \(1-\dfrac{2}{n\left(n+1\right)}=\dfrac{n\left(n+1\right)-2}{n\left(n+1\right)}=\dfrac{n^2+n-2}{n\left(n+1\right)}=\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\)
Do đó:
\(C=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}.\dfrac{3.6}{4.5}...\dfrac{38.41}{39.40}\)
\(=\dfrac{1.2.3...38}{2.3.4...39}.\dfrac{4.5.6...41}{3.4.5...40}=\dfrac{1}{39}.\dfrac{41}{3}=\dfrac{41}{117}\)