K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 3 2018
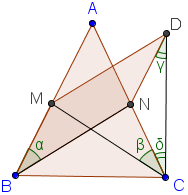
gọi 2 đường phân giác trong BN, CM bằng nhau
dựng hình bình hành BMDN và kí hiệu các góc α,β,γ,δα,β,γ,δ như hình vẽ
tam giác CMD cân tại M nên α+γ=β+δα+γ=β+δ (1)
nếu α>βα>β thì xét hai tam giác BCN và CBM có BC chung, BN=CM,CBNˆ>BCMˆ⇒CN>BMBN=CM,CBN^>BCM^⇒CN>BM
mà BM=ND⇒γ>δ⇒α+γ>β+δBM=ND⇒γ>δ⇒α+γ>β+δ, mâu thuẫn với (1)
tương tự, ko thể xảy ra trường hợp α<βα<β
suy ra α=βα=β, đpcm
30 tháng 1 2022
a: \(3x^2+y^2+10x-2xy+26=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(2x^2+10x+\dfrac{5}{2}\right)+\dfrac{47}{2}=0\)
\(\Leftrightarrow\left(x-y\right)^2+2\cdot\left(x+\dfrac{5}{2}\right)^2+\dfrac{47}{2}=0\)(vô lý)
b: \(\Leftrightarrow3x^2-12x+12+6y^2-20y+\dfrac{50}{3}+\dfrac{34}{3}=0\)
\(\Leftrightarrow3\left(x-2\right)^2+6\left(y-\dfrac{5}{3}\right)^2+\dfrac{34}{3}=0\)(vô lý)
25 tháng 4 2020
A D I E F K G B H C
Gọi I = DE \(\cap\)AH
K = FG \(\cap\)AH
a) DE // BC
=> \(\frac{AD}{AB}=\frac{DE}{BC}=\frac{AI}{AH}=\frac{1}{3}\)
=> DE = \(\frac{BC}{3}=\frac{15}{3}=5\)
FG // BC
=> \(\frac{AK}{AH}=\frac{FG}{BC}=\frac{2}{3}\)
=> FG = \(\frac{2}{3}.BC=\frac{2}{3}.15=10\)
b) SABC= \(\frac{1}{2}.AH.BC=270\)
\(\frac{1}{2}AH.15=270\)
AH =36
=> IK = \(\frac{1}{3}.AH=\frac{36}{3}=12\)
=> SDEGF = \(\frac{1}{2} \left(DE+FG\right).IK\)
= \(\frac{1}{2}.\left(5+10\right).12\)
= 90cm2
T
20 tháng 12 2016
bài 1
P= 5x2+2y2+4xy-4x+8y+25
= (4x2 +4xy+y2) + (x2-4x+4)+(y2 +8y +16)+5
= (2x+y)2+ (x-2)2+(y+4)2+5 lớn hơn hoặc bằng 5 với mọi x,y
dấu ''='' xảy ra <=> \(\begin{cases}2x+y=0\\x-2=0\\y+4=0\end{cases}\)
<=>\(\begin{cases}2x=-y\\x=2\\y=-4\end{cases}\)
<=> x= 2 và y =-4
vậy GTNN của P = 5 <=> x= 2 và y =-4
T
20 tháng 12 2016
câu 2
Giải 1.
Xét tứ giác ADHE có
góc DAE = góc ADH = góc AEH =90 độ (gt)
=> tứ giác ADHE là hình chứ nhật (dhnb)
Vậy tứ giác ADHE là hình chữ nhật
giải 2. giả sử AH cắt DE tại O . nối O với M
xét tam giác HEC vuông tại E( HE vuông góc với EC) có
EM là đường trung tuyến ứng với cạnh HC ( M là trung điểm HC)
=> EM = 1/2HC (t/c)
mà HM = 1/2 HC(M là trung điểm của HC)
=> EM=HM
Xét hình chữ nhật ADHE có : AH giao với DE tại O (gt)
=> O là trung điểm của AH và O là trung điểm DE (t/c)
mà AH=DE ( tứ giác ADHE là hình chữ nhật)
=> OH=OE
Xét tam giác OHM và tam giác OEM có
OH =OE(cmt)
HM= EM (cmt)
OM chung
do đó tam giác OHM = tam giác OEM (c-c-c)
=> góc OHM = góc OEM (2 góc tương ứng)
mà góc OHM=90 độ ( AH vuông góc với HC)=> góc OEM =90 độ hay góc DEM= 90 độ
Xét tam giác DEM có góc DEM 90 độ => tam giác DEM vuông tại E
Vậy tam giác DEM vuông tại E
giải 3: giải sử DE=2EM
mà DE= AH (cmt) và HC=2EM(cmt)
=> AH= HC
=> tam giác AHC cân tại H (dhnb) mà AHC=90 độ (AH vuông góc vs HC)
=> tam giác AHC vuông cân tại H ( dnhn)
=> góc ACH= 45 độ
Xét tam giác ABC vuông tại A có
góc ABC + góc ACB=90 độ (t/c)
=> góc ABC = 90độ - 45 độ = 45 độ
=>góc ABC = góc CAB
do đó tam giác ABC vuông cân (dhnb)
Vậy tam giác ABC vuông cân thì DE=2EM