Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì AH là đường phân giác mà tam giác ABC cân tại A
=> AH là đường trung tuyến => BH = HC
Xét tam giác AHB và tam giác AHC có :
AH _ chung
BH = HC ( cmt )
AB = AC
Vậy tam giác AHB = tam giác AHC ( c.c.c )
Vì AH là đường trung tuyến => BH = BC/2 = 3 cm
và
nãy mình ấn lộn bạn thông cảm mình nhé
và AH cũng đồng thời là đường cao
Xét tam giác AHB vuông tại H
\(AB=\sqrt{AH^2+BH^2}=\sqrt{16+9}=5cm\)
=> BA = AC = 5 cm ( do tam giác ABC cân tại A )

I A B C H E F
a, Vì △ABC cân tại A => AB = AC và ABC = ACB
Xét △BAH và △CAH cùng vuông tại H
Có: AH là cạnh chung
AB = AC (cmt)
=> △BAH = △CAH (ch-cgv)
b, Vì △BAH = △CAH (cmt)
=> BH = CH (2 cạnh tương ứng)
mà BH + CH = BC
=> BH = CH = BC : 2 = 12 : 2 = 6 (cm)
Xét △BAH vuông tại H có: AH2 + BH2 = AB2 (định lý Pytago)
=> AH2 = AB2 - BH2 = 102 - 62 = 64
=> AH = 8 (cm)
c, Vì EH // AC (gt) => ∠HAC = ∠AHE (2 góc so le trong)
Mà ∠HAC = ∠HAB (△CAH = △BAH)
=> ∠AHE = ∠HAB => ∠AHE = ∠HAE
=> △AHE cân tại E
d, Gọi { I } = EH ∩ BF
Vì HE // AC (gt) => ∠EHB = ∠ACB (2 góc đồng vị)
Mà ∠ABC = ∠ACB (cmt)
=> ∠EHB = ∠ABC => ∠EHB = ∠EBH => △EHB cân tại E => EB = EH
Mà EA = HE (△AHE cân tại E)
=> EA = BE
Xét △BAH có: E là trung điểm AB (EA = BE) => HE là đường trung tuyến
F là trung điểm AH => BF là đường trung tuyến
EH ∩ BF = { I }
=> I là trọng tâm của △BAH
\(\Rightarrow BI=\frac{2}{3}BF\) và \(HI=\frac{2}{3}EH\)
Xét △BHI có: BI + HI > BH (bđt △)
\(\Rightarrow\frac{2}{3}BF+\frac{2}{3}EH>\frac{BC}{2}\)
\(\Rightarrow\frac{2}{3}\left(BF+EH\right)>\frac{BC}{2}\)
\(\Rightarrow BF+EH>\frac{BC}{2}\div\frac{2}{3}=\frac{BC}{2}.\frac{3}{2}=\frac{3}{4}BC\) (đpcm)

c)\(\Delta\)BHA vuông tại A
=> ^ABH + ^BAH = 90 độ
mà ^BHE +^EHA = 90 độ
mà ^BAH = ^EHA ( vì \(\Delta\)AEH cân tại E)
=> ^ABH = ^BHE => \(\Delta\)BEH cân tại E
Gọi K là trung điểm BH => EK vuông BH
vì \(\Delta\)AEH cân => EF vuông AH
=> \(\Delta\)EKH = \(\Delta\)HFE => EF = KH = 1/2 BH = 1/4 BC
Ta có: \(\Delta\)EFH vuông tại F => EH > EF = 1/4 BC
\(\Delta\)BFH vuông tại H => BF > BH = 1/2 BC
=> BF + HE > 1/4 BC + 1/2 BC = 3/4 BC

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
b: BH=CH=12/2=6cm
=>AC=căn AH^2+HC^2=10cm
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H
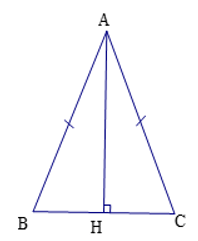
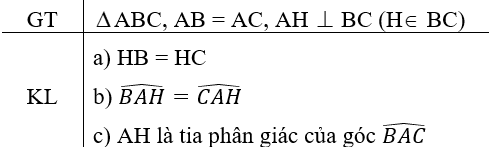
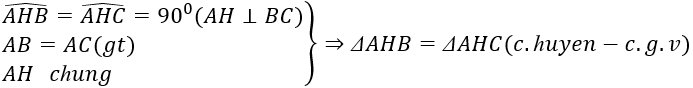
a: Xét ΔAHB và ΔAHC có
AB=AC
\(\widehat{BAH}=\widehat{CAH}\)
AH chung
Do đó: ΔAHB=ΔAHC
b: BH=BC/2=6/2=3(cm)
=>AB=5(cm)
=>AC=5(cm)