Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔADB có
\(cosA=\dfrac{AB^2+AD^2-DB^2}{2\cdot AB\cdot AD}\)
=>\(\dfrac{a^2+9a^2-DB^2}{2\cdot a\cdot3a}=\dfrac{1}{2}\)
=>\(10a^2-DB^2=3a^2\)
=>\(DB=a\sqrt{7}\)
Xét ΔABD có
\(cosABD=\dfrac{BA^2+BD^2-AD^2}{2\cdot BA\cdot BD}\)
\(=\dfrac{9a^2+7a^2-a^2}{2\cdot3a\cdot a\sqrt{7}}=\dfrac{15a^2}{6a^2\cdot\sqrt{7}}=\dfrac{15}{6\sqrt{7}}=\dfrac{5}{2\sqrt{7}}\)
=>\(cosCDB=\dfrac{5}{2\sqrt{7}}\)(do \(\widehat{ABD}=\widehat{CDB}\) vì AB//CD)
Xét ΔCDB có \(cosCDB=\dfrac{DB^2+DC^2-BC^2}{2\cdot DB\cdot DC}\)
=>\(\dfrac{5}{2\sqrt{7}}=\dfrac{7a^2+a^2-BC^2}{2\cdot a\sqrt{7}\cdot a}\)
=>\(\dfrac{8a^2-BC^2}{2a^2\sqrt{7}}=\dfrac{5}{2\sqrt{7}}\)
=>\(\dfrac{8a^2-BC^2}{a^2}=5\)
=>\(8a^2-BC^2=5a^2\)
=>\(BC^2=3a^2\)
=>\(BC=a\sqrt{3}\)

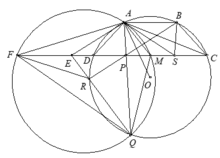
1). Gọi S điểm đối xứng với P qua M.Theo tính chất đối xứng của hình thang cân dễ thấy tứ giác ABSP cũng là hình thang cân.
Ta lại có Q P S ^ = Q A B ^ = Q R B ^ .
Từ đó có E P Q ^ = E R P ^ ⇒ Δ E R P ∽ Δ E P Q (g – g),
nên E Q P ^ = E P R ^ = B P S ^ = A S E ^ , suy ra tứ giác AEQS nội tiếp.
Do đó P A . P Q = P E . P S = P F 2 .2 P M = P F . P M , suy ra tứ giác A M Q F nội tiếp.
Từ đó suy ra đường tròn ngoại tiếp tam giác △ A Q F luôn đi qua M.

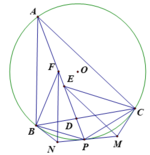
1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.