
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(a^2+ab+b^2\right)\cdot\left(a^2-ab+b^2\right)-\left(a^4+b^4\right)\)
\(=\left(a^4+b^4+2a^2b^2-a^2b^2\right)-a^4-b^4\)
\(=a^2b^2\)

17: =7x(x-y)+(x-y)=(x-y)(7x+1)
18: =(x-1)(x+x-1)=(x-1)(2x-1)
16: =4x(x-y)+3(x-y)2
=(x-y)(4x+3x-3y)
=(x-y)(7x-3y)

a: \(x^2-9y^2=\left(x-3y\right)\left(x+3y\right)\)
c: \(\left(x+5\right)^2-16=\left(x+1\right)\left(x+9\right)\)
e: \(\left(2x+3\right)^2-\left(x-7\right)^2\)
\(=\left(2x+3+x-7\right)\left(2x+3-x+7\right)\)
\(=\left(3x-4\right)\left(x+10\right)\)

a: =x^2+6x+9+x^2-6x+9+2x^2-32
=4x^2-14
b: =(x+3-10+x)^2=(2x-7)^2=4x^2-28x+49
c: =(x-3-x+5)^2=2^2=4
e: =x^2+10x+25-x^2+10x-25=20x
d: A=(5-1)(5+1)(5^2+1)(5^4+1)/4
=(5^2-1)(5^2+1)(5^4+1)/4
=(5^4-1)(5^4+1)/4
=(5^8-1)/4
g: =x^2-9-x^2-4x+5
=-4x-4

Ta có hình thoi ABCD; 2đchéo AC;BD vuông góc và cắt nhau tai TĐ O của mỗi đường
Xét tam giác vuông AOB có:
AO= 1/2 . 9,6=4,8 cm
BO=1.2 . 7,2= 3,6 cm
áp dụng định lí py ta go trong tam giác trên ta được:
AO2+BO2=AB2
=>(4,8)2+(3,6)2 =AB2
=>AB2=36=62
=>AB=6 (vì AB>0)
mà AB+BC+CD+DA
=>chu vi ht = AB+BC+CD+DA=6.4=24cm

A B C M O B' A' C' H
Từ M kẻ MH vuông góc với B'C' (H thuộc B'C')
Dễ dàng chứng minh được MH là đường trung bình của hình thang BCC'B'
=> \(MH=\frac{BB'+CC'}{2}\)
Dễ thấy tam giác OAA' = tam giác OHM (cạnh huyền - góc nhọn)
=> AA' = MH
=> \(BB'+CC'=2AA'\)
Bạn xem lại đề bài.

Ta có: \(\widehat{B}+\widehat{D}+\widehat{C}+\widehat{A}=360^0\)
\(\Rightarrow\widehat{B}+\widehat{D}=360^0-90^0-150^0=120^0\)
\(\Rightarrow3x=120^0\Rightarrow x=40^0\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{B}=2x-2.40^0=80^0\\\widehat{D}=x=40^0\end{matrix}\right.\)
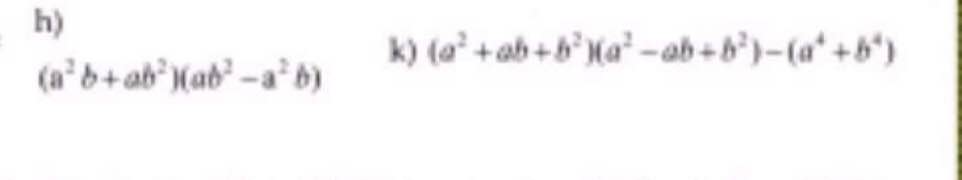
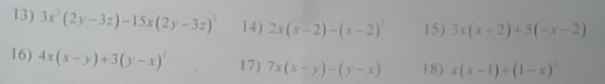
 mn giúp mik bài này với ạ này là hằng đẳng thúc ạ(ảnh hơi mờ mn thông cảm)
mn giúp mik bài này với ạ này là hằng đẳng thúc ạ(ảnh hơi mờ mn thông cảm)