K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 10 2016
Hình 31 cho biết hai tia AM và AN đối nhau, góc tia AO nằn giữa hai tia AN và AP , Hãy tính số đo x của
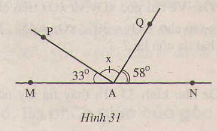
Giải:= 1800 -330 = 1470
x= 1470 -580 =-890
14 tháng 3 2017
d, \(\dfrac{-31}{240}\) e , \(\dfrac{43}{72}\) g, \(\dfrac{-5}{36}\)
NT
1
29 tháng 11 2016
a , \(\frac{3.5}{8.24}=\frac{3.5}{8.8.3}=\frac{5}{64}\)
b , \(\frac{2.14}{7.8}=\frac{2.2.7}{7.2.2.2}=\frac{1}{2}\)
c, \(\frac{3.7.11}{22.9}=\frac{3.7.11}{2.11.3}=\frac{7}{6}\)
d , \(\frac{8.5-8.2}{16}=\frac{8.\left(5-2\right)}{8.2}=\frac{8.3}{8.2}=\frac{3}{2}\)
e , \(\frac{11.4-11}{2-13}=\frac{11.\left(4-1\right)}{-11}=\frac{11.3}{-11}=-3\)
BB
9 tháng 2 2017
\(a,\frac{a}{-b}=\frac{-a}{b}vìa.b=-a.\left(-b\right)\)
\(b,\frac{-a}{-b}=\frac{a}{b}vì-a.b=-b.a\)
NM
2
20 tháng 3 2017
C=c.3/4+c.5/6-c.19/12
=c.(3/4+5/6-19/12)
=c.0
=0
Vậy C=0
AY
21 tháng 3 2017
Thay c = 2002/2003 vào, ta có:
C = 2002/2003 . 3/4 + 2002/2003 . 5/6 - 2002/2003 . 19/12
C = 2002/2003 . (3/4 + 5/6 - 19/12)
C = 2002/2003 . (9/12 + 10/12 - 19/12)
C = 2002/2003 . 0
C = 0
DM
29 tháng 11 2016
a) \(\frac{3\cdot5}{8\cdot24}=\frac{5}{8\cdot8}=\frac{5}{64}\)
b) \(\frac{2\cdot14}{7\cdot8}=\frac{14}{7\cdot4}=\frac{2}{4}=\frac{1}{2}\)
c) \(\frac{3\cdot7\cdot11}{22\cdot9}=\frac{7}{2\cdot3}=\frac{7}{6}\)
d) \(\frac{8\cdot5-8\cdot2}{16}=\frac{8\cdot3}{16}=\frac{24}{16}=\frac{3}{2}\)
e) \(\frac{11\cdot4-11}{2-13}=\frac{11\cdot3}{2-13}=\frac{33}{-11}=-3\)
22 tháng 10 2016
Gọi Ot, Ot' là hai tia nằm trên cùng một nửa mặt phẳng bờ là đường thẳng xy đi qua O. Biết = 300 ,
= 600
. Tính số đo các góc yOt, tOt'.
Giải:
Hai góc xOt và yOt kề bù nên:
= 1800 -
= 1800 - 300 = 1500
Hai tia Ot' và Ot cùng thuộc nửa mặt phẳng bờ Oy mà <
nên tia Ot' nằm giữa hai tia Oy và Ot, suy ra
nên tia Ot' nằm giữa hai tia Oy và Ot, suy ra : +
=
Thay số ta được: 600+ 600 = 1500
Suy ra:
= 900
CH
6
IM
12 tháng 8 2016
\(\left|3\right|< \left|5\right|\)
\(\left|-1\right|>\left|0\right|\)
\(\left|-3\right|< \left|-5\right|\)
\(\left|2\right|=\left|-2\right|\)
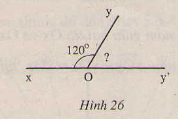
Hình 26 cho biết hai góc kề bù xOy và yOy',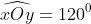
. Tính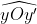 
Giải:
Hai góc xOy và yOy' kề bù nên
suy ra: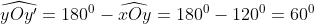
Có: \(\widehat{xOy}+\widehat{yOy'}=180^o\)
=> \(\widehat{yOy'}=180-\widehat{xOy}=180-120=60\)