
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:\(2009^{20}=\left(2009^2\right)^{10}=4036081^{10}< 20092009^{10}\)
Vậy \(2009^{20}< 20092009^{10}\)

Theo mình nghĩ thì đề thiếu là tam giác ABC vuông tại A nhé!
Bạn xem lại đề!:)

Giải:
a) Có: \(0,\left(37\right)=0,373737373737...\)
\(0,\left(62\right)=0,626262626262...\)
\(\Leftrightarrow0,\left(37\right)+0,\left(62\right)=0,99999999999...\)
Mà \(0,9999999999999...\simeq1\)
Hay \(0,\left(9\right)=1\)
Vậy \(0,\left(37\right)+0,\left(62\right)=1\).
b) \(0,\left(33\right).3=0,99999...=0,\left(9\right)=1\)
Vậy \(0,\left(33\right).3=1\).
Chúc bạn học tốt!!!
\(a)0,\left(37\right)=0,37373737....\)
\(0,\left(62\right)=0,62626262....\)\(\Leftrightarrow0,\left(37\right)+0,\left(62\right)=0,99999999....\)
Mà \(0,99999999....\simeq1\)
hoặc \(0,\left(9\right)\simeq1\)
\(\Rightarrow0,\left(37\right)+\left(0,62\right)=1\)
\(b)0,\left(33\right).3=1\)
\(\Leftrightarrow0,99999999....=0,\left(9\right)\simeq1\)
\(\Rightarrow0,\left(33\right).3=1\)
Chúc bạn học tốt!

\(xy-x-y+1=0\)
\(\Rightarrow x.\left(y-1\right)-\left(y-1\right)=0\)
\(\Rightarrow\left(y-1\right).\left(x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}y-1=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
Vậy \(x=y=1\)
Chúc bạn học tốt!!!
Tìm x,y biết:
xy-x-y+1=0
=> x(y-1)-y=0-1
=> x(y-1)- (y-1)= (-1)
=> (y-1)(x-1)=(-1)
\(\Rightarrow\left[{}\begin{matrix}y-1=1;x-1=-1\\y-1=-1;x-1=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=2;x=0\\y=0;x=2\end{matrix}\right.\)

2.
a) +) ta co: tam giác GLO
GL = 6, LO = 8, OG = 10
=> GL < LO < GO ( 6<8<10)
=> góc O < góc G < góc L ( quan hệ giữa góc và cạnh đối diện trong tam giác LOG )
+) ta co: tam giac UVW
góc V = 40, góc U = 50
=> góc W = 180 - ( góc V + goc Ư )
= 180 - ( 50 + 40)
= 90
=> góc V < góc U < góc W
=> UW < VW < VU ( quan hệ giữa cạnh và góc trong tam giác ACB )

\(\left(\dfrac{-5}{13}\right)^{2017}\cdot\left(\dfrac{13}{5}\right)^{2016}=\left(\dfrac{-5}{13}\right)\cdot\left(-\dfrac{5}{13}\right)^{2016}\cdot\left(\dfrac{13}{5}\right)^{2016}=\left(\dfrac{-5}{13}\right)\cdot\left(\dfrac{5}{13}\right)^{2016}\cdot\left(\dfrac{13}{5}\right)^{2016}=\left(-\dfrac{5}{13}\right)\cdot\left[\left(\dfrac{5}{13}\right)^{2016}\cdot\left(\dfrac{13}{5}\right)^{2016}\right]=\left(-\dfrac{5}{13}\right)\cdot1^{2016}=\left(-\dfrac{5}{13}\right)\cdot1=-\dfrac{5}{13}\)
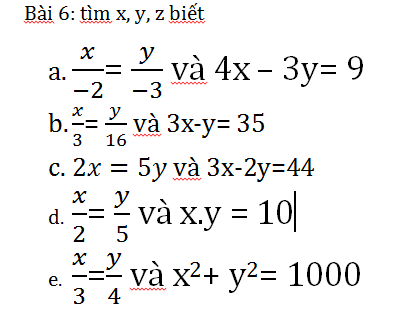









Bài 6 :
a ) \(\frac{x}{-2}=\frac{y}{-3}\) và \(4x-3y=9\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{-2}=\frac{y}{-3}=\frac{4x}{-8}=\frac{3y}{-9}=\frac{4x-3y}{-8-\left(-9\right)}=\frac{9}{1}=9\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{-2}=9\\\frac{y}{-3}=9\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-18\\y=-27\end{cases}}\)
b ) \(\frac{x}{3}=\frac{y}{16}\)và \(3x-y=35\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{16}=\frac{3x}{9}=\frac{y}{16}=\frac{3x-y}{9-16}=\frac{35}{-7}=-5\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{3}=-5\\\frac{y}{16}=-5\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-15\\y=-80\end{cases}}\)
c ) \(2x=5y\)và \(3x-2y=44\)
Từ \(2x=5y\)\(\Rightarrow\)\(\frac{x}{5}=\frac{y}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{5}=\frac{y}{2}=\frac{3x}{15}=\frac{2y}{4}=\frac{3x-2y}{15-4}=\frac{44}{11}=4\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{5}=4\\\frac{y}{2}=4\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=20\\y=8\end{cases}}\)
d ) \(\frac{x}{2}=\frac{y}{5}\)và \(xy=10\)
Đặt \(\frac{x}{2}=\frac{y}{5}=k\)
\(\Rightarrow\hept{\begin{cases}x=2k\\y=5k\end{cases}}\)
Thay vào ta có :
\(2k.5k=10\)
\(10.k^2=10\)
\(k^2=1\)
\(k=\pm1\)
+ Nếu \(k=1\)\(\Rightarrow\hept{\begin{cases}x=2.1=2\\y=5.1=5\end{cases}}\)
+ Nếu \(k=-1\)\(\Rightarrow\hept{\begin{cases}x=2.\left(-1\right)=-2\\y=5.\left(-1\right)=-5\end{cases}}\)
e ) \(\frac{x}{3}=\frac{y}{4}\)và \(x^2+y^2=1000\)
Đặt \(\frac{x}{3}=\frac{y}{4}=k\)
\(\Rightarrow\hept{\begin{cases}x=3k\\y=4k\end{cases}}\)
Thay vào ta có :
\(\left(3k\right)^2+\left(4k\right)^2=1000\)
\(3^2.k^2+4^2.k^2=1000\)
\(9.k^2+16.k^2=1000\)
\(25.k^2=1000\)
\(k^2=40\)
Phần sau bạn xem lại đề nhé ;-;"