Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số sản phẩm tổ 1 được giao theo kế hoạch là x(sản phẩm), số sản phẩm tổ 2 được giao theo kế hoạch là y(sản phẩm)
(ĐIều kiện: \(x,y\in Z^+\))
Theo kế hoạch, hai đội được giao 2400 sản phẩm nên
x+y=2400(1)
Số sản phẩm đội 1 làm được là x(1+15%)=1,15x(sản phẩm)
Số sản phẩm đội 2 làm được là:
y(1+12%)=1,12y(sản phẩm)
Thực tế hai đội làm được 2733 sản phẩm nên 1,15x+1,12y=2733(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=2400\\1,15x+1,12y=2733\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}1,15x+1,15y=2760\\1,15x+1,12y=2733\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}0,03y=27\\x+y=2400\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=900\\x=2400-900=1500\end{matrix}\right.\left(nhận\right)\)
vậy: Số sản phẩm được theo kế hoạch của đội 1 và đội 2 lần lượt là 1500 sản phẩm và 900 sản phẩm

Gọi số sản phẩm đội dự định làm mỗi ngày là x (x ∈ ℕ * , x < 84) (sản phẩm)
*) Theo kế hoạch, thời gian hoàn thành là 1000/x (ngày)
*) Thực tế, mỗi ngày làm được x + 10 (sản phẩm)
Thời gian hoàn thành 1000/(x+10) (ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
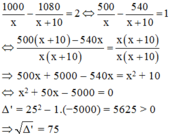
Phương trình có hai nghiệm phân biệt: x 1 = − 25 – 75 = −100 (loại)
và x 2 = −25 + 75 = 50 (tmđk)
Vậy theo kế hoạch, mỗi ngày tổ dự định làm 50 sản phẩm
Đáp án: C

Bài 1 :
Gọi số người của đội là \(x\) người \(\left(x\inℕ^∗\right)\)
Thời gian làm theo kế hoạch là \(\frac{420}{x}\) ngày
Số người lúc sau là \(x+5\) người
Thời gian hoàn thành lúc sau là \(\frac{420}{x+5}\) ngày
Vì thời gian giảm 7 ngày nên ta có phương trình :
\(\frac{420}{x}-7=\frac{420}{x+5}\)
\(\Leftrightarrow420\left(x+5\right)-7x\left(x+5\right)=420x\)
\(\Leftrightarrow420x+2100-7x^2-35x-420x\)
\(\Leftrightarrow7x^2+35x-2100=0\)
\(\Leftrightarrow x^2+5x-300=0\)
\(\Leftrightarrow\left(x+20\right)\left(x-15\right)=0\)
\(\Leftrightarrow x=15\) \(\left(x\inℕ^∗\right)\)
Vậy số người của đội là 15 người.

Gọi số sản phẩm làm theo kế hoạch mỗi ngày là x>0 và số ngày dự định là y>0
Ta có: \(xy=200\)
4 ngày đầu làm được: \(4x\) sản phẩm
Những ngày còn lại: \(\left(y-6\right)\left(x+10\right)\)
Theo bài ra ta có hệ:
\(\left\{{}\begin{matrix}xy=200\\4x+\left(y-6\right)\left(x+10\right)=200\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=200\\5y-x=30\end{matrix}\right.\)
\(\Rightarrow y\left(5y-30\right)=200\)
\(\Leftrightarrow y^2-6y-40=0\Rightarrow\left[{}\begin{matrix}y=10\\y=-4\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{200}{10}=20\)

Lời giải:
Gọi số sản phẩm tổ 1, 2 làm theo kế hoạch là $a,b$ (sản phẩm)
Tổng số sản phẩm phải làm: $a+b=900(1)$
Tổng số sản phẩm thực tế: $1,2a+1,3b=1130(2)$
Từ $(1); (2)\Rightarrow a=400; b=500$

Gọi số sản phẩm tổ 1 phải làm là x
số sản phẩm tổ 2 phải làm là y ( x, y thuộc N* ; x, y < 900 )
Theo đề bài ta có : x + y = 900 ( 1 )
Tổ 1 vượt mức kế hoạch 20%, tổ 2 vượt mức kế hoạch 30% nên hai tổ làm được 1130
tức là ( x + 20% ) + ( y + 30%y ) = 1130
<=> ( x + 1/5x ) + ( y + 3/10y ) = 1130
<=> x( 1 + 1/5 ) + y( 1 + 3/10 ) = 1130
<=> 6/5x + 13/10y = 1130 (2)
Từ (1) và (2) => Ta có hệ phương trình :
\(\hept{\begin{cases}x+y=900\\\frac{6}{5}x+\frac{13}{10}y=1130\end{cases}}\)
Nhân 6/5 vào từng vế của (1)
\(\Leftrightarrow\hept{\begin{cases}\frac{6}{5}x+\frac{6}{5}y=1080\left(3\right)\\\frac{6}{5}x+\frac{13}{10}y=1130\end{cases}}\)
Lấy (3) trừ (2) theo vế
\(\Leftrightarrow-\frac{1}{10}y=-50\Leftrightarrow y=500\)(tmđk)
Thế y = 500 vào (1)
\(\Leftrightarrow x+500=900\Leftrightarrow x=400\)(tmđk)
Vậy theo kế hoạch, tổ 1 phải làm 400 sản phẩm
tổ 2 phải làm 500 sản phẩm
Gọi sản phẩm tổ 1 là x
tổ 2 là y
Hệ pt x+y=900
( 20x/100 + x) +( 30y/100 +y)=1130
=» x =400 y=500

Gọi a ( sản phẩm ) là số sản phẩm tổ 1 phải làm theo kế hoạch
Điều kiện : 0 < x < 800 , x \(\varepsilon\)Z
800 - x là số sản phẩm tổ 2 phải làm theo kế hoạch
0,1 x là số sản phẩm tổ 1 làm thêm được
0,2 ( 800 - x ) là số sản phẩm tổ 2 làm thêm được
Vì cả 2 tổ làm thêm được 110 ( 910 - 800 = 110 ) nên ta có :
0,1 x + 0,2 ( 800 - x ) = 110
=> 0,1 x - 160 - 0,2x = 110
=> 0,1 x = 50
=> x = 500 ( tmđk )
Vậy theo kế hoạch tổ 1 phải làm 500 sản phẩm
Tổ 2 phải làm 300 sản phẩm ( 800 - 500 = 300 )
Gọi số sản phẩm tổ 1 làm là x
số sản phẩm tổ 2 làm là y ( x, y thuộc N* ; x, y < 800 )
Theo đề bài ta có :
x + y = 800 ( 1 )
( x + 10%x ) + ( y + 20%y ) = 910
<=> ( x + 1/10x ) + ( y + 1/5y ) = 910
<=> x( 1 + 1/10 ) + y( 1 +1/5 ) = 910
<=> 11/10x + 6/5y = 910 ( 2 )
Từ (1) và (2) => Ta có hệ phương trình :
\(\hept{\begin{cases}x+y=800\\\frac{11}{10}x+\frac{6}{5}y=910\end{cases}}\)
Nhân 11/10 vào từng vế của (1)
\(\Rightarrow\hept{\begin{cases}\frac{11}{10}x+\frac{11}{10}y=880\left(3\right)\\\frac{11}{10}x+\frac{6}{5}y=910\end{cases}}\)
Lấy (3) trừ (2) theo vế
\(\Rightarrow-\frac{1}{10}y=-30\Rightarrow y=300\)
Thế y = 300 vào (1)
\(\Rightarrow x+300=800\Rightarrow x=500\)
Cả hai giá trị đều tmđk
Vậy : Tổ 1 làm được 500 sản phẩm
Tổ 2 làm được 300 sản phẩm

gọi x là số sản phẩm làm 1 ngày theo dự định
3200/x là số ngày làm 3200 sp theo dự định
5+(3200-5x)/(x+40) là số ngày làm xong sản phẩm thực tê
ta có pt
3200/x-3=(5+(3200-5x)/(x+40))
pt \(\frac{20x}{100}+\frac{15\left(1300-x\right)}{100}=1515-1300\)
Gọi x(sản phẩm ) là số sản phẩm mà đội 1 phải hoàn thành theo kế hoạch
ĐK 1300>x>0
Số sản phẩm mà đội hai làm theo kế hoạc là 1300-x (sp)
số sản phẩm của đội một sau khi tăng 20%
\(\frac{20x}{100}\) (sp)\
số sp dội ahi sau khi tăng 15%
\(\frac{15\left(1300-x\right)}{100}\) (sp)
Theo đề bài có pt