Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Theo định luật bảo toàn động lượng:
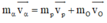
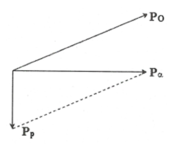
Các vectơ được biểu diễn trên hình vẽ. Từ đó ta có:
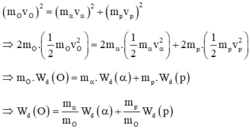
Theo định luật bảo toàn năng lượng:
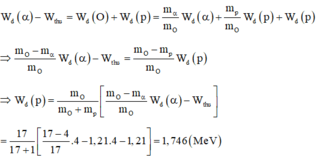

Đáp án B.
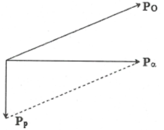
Theo định luật bảo toàn động lượng:
m α v α → = m p v p → + m 0 v o →
Các vectơ được biểu diễn trên hình vẽ. Từ đó ta có:
m o v o 2 = m α v α 2 + m p v p 2 ⇒ 2 m o . 1 2 m 0 . v 2 0 = 2 m α . 1 2 m α . v 2 α + 2 m p . 1 2 m p v 2 p ⇒ m o w d O = m α . w d α + m p . w d P ⇒ w d O = m α m o w d α + m p m o w d P
Theo định luật bảo toàn năng lượng:
w d α - w t h u = w d O + w d P = m α m o w d α + m p m o w d ( P ) + w d P ⇒ m o - m α m o w d α - w t h u = m o - m p m o w d P ⇒ w d P = m 0 m 0 + m p = m o - m α m o w d α - w t h u = 17 17 + 1 17 - 4 17 . 4 - 1 , 21 . 4 - 1 , 21 = 1 , 746 ( M e v )

Đáp án B
Động năng của proton: K 1 = K 2 + K 3 - ∆ E = 5 , 48 M e V
Gọi p là động lượng của của một vật; p = m v ; K = m v 2 2 = p 2 2 m
![]()
Theo định luật bảo toàn động lượng thì p 1 = p 2 + p 3
![]()
Suy ra 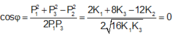
Vậy nên φ = π 2

Đáp án B.
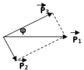
Động năng của proton: K1 = K2 + K3 - ∆E = 5,48 MeV
Gọi P là động lượng của một vật; P = mv; ![]()
P12 = 2m1K1 = 2uK1; P22 = 2m2K2 = 12uK2 ; P32 = 2m3K3 = 8uK3
![]()
![]()
![]()
![]()

Phương pháp: Sử dụng định luật bảo toàn động lượng.
Cách giải: Ta có thể biểu diễn các vecto động lượng như hình vẽ:
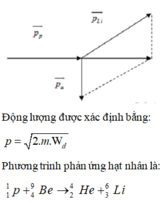
Áp dụng định luật bảo toàn động lượng cho hệ hai hạt p và Be.
![]()
Gọi góc giữa vec to động lượng của Li và vecto tổng động lượng là α. Ta có
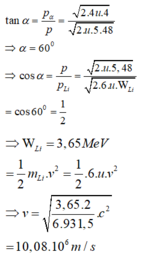
Đáp án A


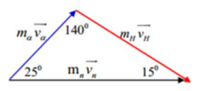
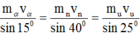
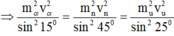
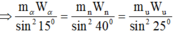
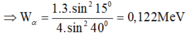
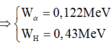
+ B1: Bạn dùng định luật bảo toàn động lượng \(\vec{p_{trước}}=\vec{p_{sau}}\)
+ B2: Bạn chuyển các véc tơ động lượng của các hạt muốn tính góc về 1 vế.
+ B3: Bạn bình phương 2 vế, sẽ xuất hiện cos góc giữa 2 hạt, và chuyển về biểu thức động năng rồi tính.