
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1 :
a ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{12}=\frac{y}{-8}=\frac{x+y}{12+\left(-8\right)}=\frac{-48}{4}=-12.\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{12}=-12\\\frac{y}{-8}=-12\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-144\\y=96\end{cases}}\)
b ) Từ \(x\):\(\left(-7\right)\)= \(y\): \(10\)
\(\Rightarrow\)\(\frac{x}{-7}=\frac{y}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{-7}=\frac{y}{10}=\frac{y-x}{10-\left(-7\right)}=\frac{-34}{17}=-2\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{-7}=-2\\\frac{y}{10}=-2\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=14\\y=-20\end{cases}}\)
c ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{15}=\frac{y}{-12}=\frac{2x}{30}=\frac{y}{-12}=\frac{2x+y}{30+\left(-12\right)}=\frac{-360}{18}=-20\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{15}=-20\\\frac{y}{-12}=-20\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-300\\y=240\end{cases}}\)
d ) Từ \(2x=-3y\)\(\Rightarrow\)\(\frac{x}{-3}=\frac{y}{2}\)
Áp dugj tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{-3}=\frac{y}{2}=\frac{x}{-3}=\frac{5y}{10}=\frac{x-5y}{-3-10}=\frac{-130}{-13}=10\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{-3}=10\\\frac{y}{2}=10\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-30\\y=20\end{cases}}\)
Bài 2 :
a ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{2}=\frac{y}{-3}=\frac{z}{5}=\frac{x+y-z}{2+\left(-3\right)-5}=\frac{-54}{-6}=9.\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{2}=9\\\frac{y}{-3}=9\\\frac{z}{5}=9\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=18\\y=-27\\z=45\end{cases}}\)
b ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{4}=\frac{y}{-7}=\frac{z}{3}=\frac{x}{4}=\frac{2y}{-14}=\frac{z}{3}=\frac{x+2y-z}{4+\left(-14\right)-3}=\frac{-39}{-13}=3\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{4}=3\\\frac{y}{-7}=3\\\frac{z}{3}=3\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=12\\y=-21\\z=9\end{cases}}\)





a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
BD=CE
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: ΔABD=ΔACE
Suy ra: AB=AC
hay ΔABC cân tại A
b: XétΔABC có
AD là đường cao
CH là đường cao
AD cắt CH tại D
Do đó: D là trực tâm của ΔABC
=>BD vuông góc với AC
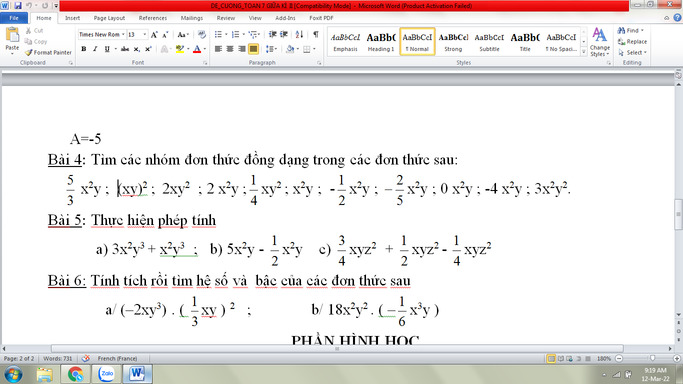




 Giải giúp mình bài 4, 5, 7 với ạ, mình cảm ơn trước ;-;
Giải giúp mình bài 4, 5, 7 với ạ, mình cảm ơn trước ;-;











Bài 5:
a: \(=4x^2y^3\)
b: \(=\dfrac{9}{2}x^2y\)
c: \(=xyz^2\left(\dfrac{3}{4}-\dfrac{1}{4}+\dfrac{1}{2}\right)=xyz^2\)
Bài 4
Nhóm 1: \(\dfrac{5}{3}x^2y,2x^2y,x^2y,\dfrac{1}{2}x^2y,\dfrac{-1}{2}x^2y,\dfrac{-2}{5}x^2y,0x^2y,-4x^2y\)
Nhóm 2: \(\left(xy\right)^2,3x^2y^2\)
Bài 5
\(a,3x^2y^3+x^2y^3\)
\(=4x^2y^3\)
\(b,5x^2y-\dfrac{1}{2}x^2y\)
\(=\left(5-\dfrac{1}{2}\right)\left(x^2y\right)\)
\(=\dfrac{9}{2}x^2y\)
\(c,\dfrac{3}{4}xyz^2+\dfrac{1}{2}xyz^2-\dfrac{1}{4}xyz^2\)
\(=\left(\dfrac{3}{4}+\dfrac{1}{2}-\dfrac{1}{4}\right)\left(xyz^2\right)\)
\(=\left(\dfrac{3}{4}+\dfrac{2}{4}-\dfrac{1}{4}\right)\left(xyz^2\right)\)
\(=xyz^2\)
Bài 6
\(a,\left(-2xy^3\right)\left(\dfrac{1}{3}xy\right)^2\)
\(=\left(-2.\dfrac{1}{9}\right)\left(x.x^2\right)\left(y^3y^2\right)\)
\(=\dfrac{-2}{9}x^3y^5\)
Bậc: 3 + 5 = 8
Hệ số: \(\dfrac{-2}{9}\)
\(b,18x^2y^2\left(\dfrac{-1}{6}x^3y\right)\)
\(=\left(-18.\dfrac{1}{6}a\right)\left(x^2x^2\right)\left(y^2y^3\right)\)
\(=-3ax^4y^5\)
Bậc: 4 + 5 = 9
Hệ số: \(-3a\)