
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


mk nghĩ là nếu nhún thì sẽ có đà nhảy lên nhưng mà k nhún vẫn có thể nhảy lên mà =)) haha
ht
ht
ht
ht
ht
TL:
Nếu không nhún chân khi nhảy lên thì sẽ không có lực để có thể nhảy lên
Mik ko chắc nha
@@@@@@
HT

Hợp lực của lực căng dây \(\overrightarrow T \)và trọng lực \(\overrightarrow P \):
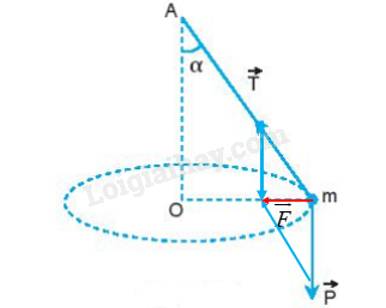
Lực hướng tâm chính là hợp lực của \(\overrightarrow T \)và \(\overrightarrow P \).



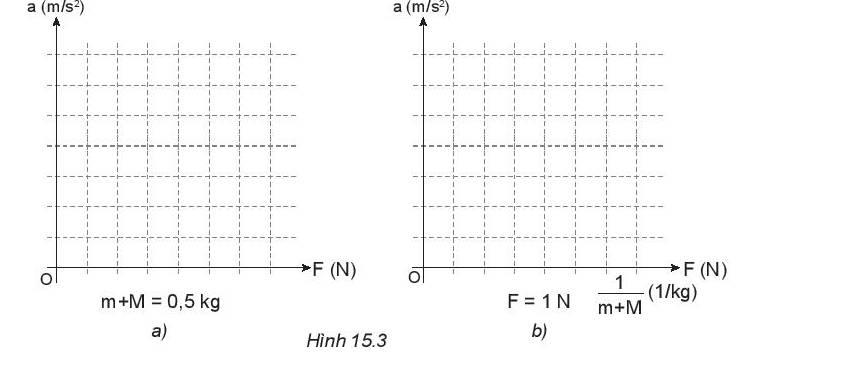
a)
- a phụ thuộc vào F (m + M = 0, 5kg)
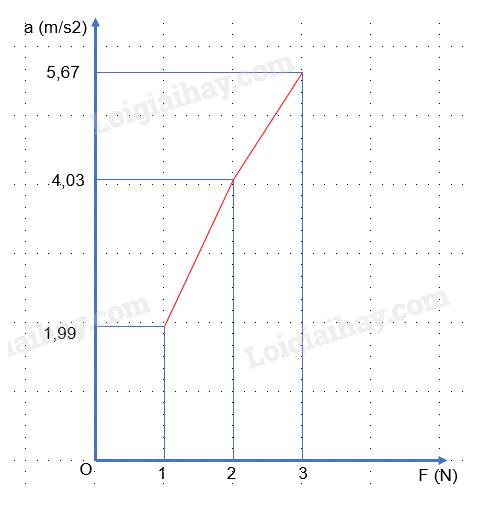
Ta có:
+ Khi F = 1 N, a = 1,99 m/s2 thì \(\frac{F}{a} = \frac{1}{{1,99}} \approx 0,5\)
+ Khi F = 2 N, a = 4,03 m/s2 thì \(\frac{F}{a} = \frac{2}{{4,03}} \approx 0,5\)
+ Khi F = 3 N, a = 5,67 m/s2 thì \(\frac{F}{a} = \frac{3}{{5,67}} \approx 0,5\)
=> Tỉ số \(\frac{F}{a}\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào F là một đường thẳng
- a phụ thuộc vào \(\frac{1}{{m + M}}\) (ứng với F = 1 N)
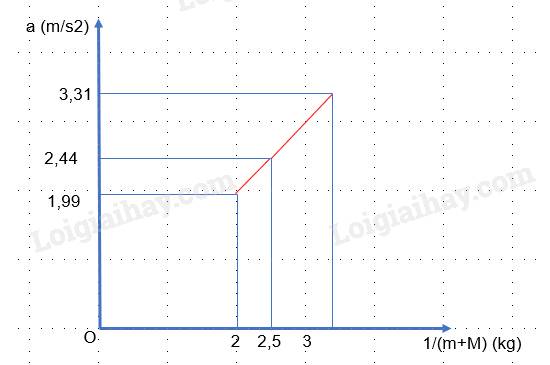
Ta có:
+ Khi a = 3,31 m/s2 , \(\frac{1}{{M + m}} = \frac{{10}}{3}\) thì a. (M + m) = 1
+ Khi a = 2,44 m/s2 , \(\frac{1}{{M + m}} = 2,5\) thì a. (M + m) = 1
+ Khi a = 1,99 m/s2 , \(\frac{1}{{M + m}} = 2\) thì a. (M + m) = 1
=> Tỉ số \(\frac{a}{{\frac{1}{{M + m}}}} = a.(M + m)\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào \(\frac{1}{{M + m}}\) là một đường thẳng.
b) Ta có:
+ Khi (m + M) không đổi, F tăng thì a cũng tăng => Gia tốc a tỉ lệ thuận với lực F
+ Khi F không đổi, a giảm thì (m+M) tăng => Gia tốc a tỉ lệ nghịch với khối lượng
=> Kết luận: Gia tốc tỉ lệ thuận với lực tác dụng và tỉ lệ nghịch với khối lượng.

1.47
Tóm tắt ; a=g=10m/s^2( gia tốc của rơi tự do là g=9,81m/s^2 nhưng mk lấy là 10m/s^2 cho tròn số )
t1=5s
t2=3s
a) S1(chiều dài giêngs)=?
b)V=? (vận tốc của vật khi chạm đất )
c)S2(quảng đường vật rơi sau 3s)=?
Giải
a) S1=1/2.g.t1^2=1/2.10.5^2=125(m)
b)V=at=10.5=50(m/s)
c) S2=1/2.g.t2^2=1/2.10.3^2=45(m)
1.47
a) h = 1/2 gt2= 1/2.10.52= 125m
b) v= gt = 10.5 = 50m/s
c) quãng đường vật rơi trong 3s:
s1= 1/2gt2 = 1/2.10.32= 45m
quãng đường vật rơi trong 2s:
s2= 1/2gt2= 1/2.10.22= 20m
quãng đường vật rơi trong giây thứ 3 là:
s = s1 - s2 = 45 - 20 = 25m

2.4
gia tốc của hệ
\(\overrightarrow{a}=\dfrac{\overrightarrow{P_a}+\overrightarrow{P_b}+\overrightarrow{Q_a}+\overrightarrow{Q_b}+\overrightarrow{F_{msa}}+\overrightarrow{F_{msb}}}{m_a+m_b}\)
chiếu trên trục Ox có phương sogn song với mặt phẳng nghiêng chiều dương cùng chiều chuyển động
a=\(\dfrac{sin\alpha.P_a+sin\alpha.P_b-F_{msa}-F_{msb}}{m_1+m_2}\)
\(\Leftrightarrow a=sin\alpha.m_a.g+sin\alpha.m_b.g-k_a.cos\alpha m_a.g\)\(-k_b.cos\alpha.m_b.g\))/(m1+m2)
\(\Leftrightarrow\)\(a=\left(\dfrac{sin\alpha\left(m_a+m_b\right).g-cos\alpha.g\left(k_a.m_a+k_b.m_b\right)}{m_a+m_b}\right)\)
xét riêng vật A: các lực tác dụng vào A, trọng lực Pa, phản lực Qa, lực ma sát Fmsa, lực do vật B tác dụng vào khi trượt xuống F cùng chiều chuyển động
\(\overrightarrow{F}+\overrightarrow{Q_a}+\overrightarrow{P_a}+\overrightarrow{F_{msa}}=m.\overrightarrow{a}\)
chiếu lên chiều dương cùng chiều chuyển động phương sogn song với mặt phẳng
F=\(\dfrac{g.cos\alpha.\left(k_a-k_b\right).m_b.m_a}{m_a+m_b}\)
b) để hai vật trượt xuống a\(\ge\)0
\(\Leftrightarrow\)..........
2.4
b)
\(a\ge0\)
\(\Leftrightarrow\)sin\(\alpha.\left(m_a+m_b\right).g\ge g.cos\alpha.\left(k_a.m_a+k_b.m_b\right)\)
\(\Rightarrow tan\alpha\ge\dfrac{\left(k_a.m_a+k_b.m_b\right)}{\left(m_a+m_b\right)}\Rightarrow\alpha\ge....\)

















 G
G
Câu 18.7.
Chọn hệ trục tọa độ Oxxy như hình.
Áp dụng định luật II Niuton ta có: \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=\overrightarrow{0}\)
\(Oy:N-Pcos\alpha-Fsin\alpha=0\) \(\Rightarrow N=Pcos\alpha+Fsin\alpha\)
Có \(F_{ms}=k\cdot N=k\cdot\left(Pcos\alpha+Fsin\alpha\right)=k\cdot\left(mgcos\alpha+Fsin\alpha\right)\)
\(Ox:Psin\alpha-Fcos\alpha-F_{ms}=0\)
\(\Rightarrow Fcos\alpha=Psin\alpha-F_{ms}=mgsin\alpha-k\left(mgcos\alpha+Fsin\alpha\right)\)
\(\Rightarrow F\left(cos\alpha+k.sin\alpha\right)=mg\left(sin\alpha-kcos\alpha\right)\)
\(\Rightarrow\left\{{}\begin{matrix}F_{min}=\dfrac{mg\left(sin\alpha-kcos\alpha\right)}{cos\alpha+ksin\alpha}=\dfrac{mg\left(tg\alpha-k\right)}{1+k.tg\alpha}\\F_{max}=\dfrac{mg\left(tg\alpha+k\right)}{1-k.tg\alpha}\end{matrix}\right.\)
Câu 18.8.
Chọn hệ trục tọa độ Oxy như hình vẽ.
Áp dụng định luật II Niuton: \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=\overrightarrow{0}\) \(\left(1\right)\)
\(Ox:Fcos\beta-Psin\alpha-F_{ms}=0\Rightarrow F_{ms}=Psin\alpha-Fcos\beta\)
\(Oy:N+Fsin\beta-Pcos\alpha=0\Rightarrow N=Pcos\alpha-Fsin\beta\)
Thay lần lượt vào \(\left(1\right)\) ta được:
\(F+P+Pcos\alpha-Fsin\beta+Psin\alpha-Fcos\beta=0\)
\(\Rightarrow F\left(cos\beta+sin\beta\right)=P\left(cos\alpha+sin\alpha\right)\)
Để \(F_{min}\Leftrightarrow\left(cos\beta+sin\beta\right)_{max}=tan\beta\)
\(\Rightarrow\beta=arctan\left(cos\beta+sin\beta\right)\)
Đặt \(cos\beta+sin\beta=k\)
Khi đó: \(\beta=arctank=arctgk\)