Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(R_1ntR_2\Rightarrow R_{12}=R_1+R_2=15+12=27\Omega\)
\(I=\dfrac{U}{R}=\dfrac{18}{27}=\dfrac{2}{3}A\)
Công suất toả nhiệt: \(P=U\cdot I=RI^2=27\cdot\left(\dfrac{2}{3}\right)^2=12W\)
b)\(R_3//\left(R_1ntR_2\right)\Rightarrow R_{tđ}=\dfrac{R_{12}\cdot R_3}{R_{12}+R_3}\)
\(P_{AB}=24W\Rightarrow R_{tđ}=\dfrac{U^2}{P}=\dfrac{18^2}{24}=13,5\Omega\)
\(\Rightarrow\dfrac{R_{12}\cdot R_3}{R_{12}+R_3}=13,5\Rightarrow\dfrac{27\cdot R_3}{27+R_3}=13,5\)
\(\Rightarrow R_3=27\Omega\)

a. Điện trở tương đương của mạch là: R t đ = R 1 + R 2 = 40 ω
Cường độ dòng điện chạy trong mạch là:
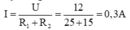
Công suất tỏa nhiệt của mạch là: P = U.I = 12. 0,3 = 3,6W
b. Đổi S = 0 , 06 m m 2 = 0 , 06 . 10 - 6 m 2
Công thức tính điện trở:
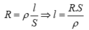
Thay số vào: 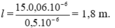

a) R1ntR2=>Rtđ=R1+R2=40\(\Omega\)=>I1=I2=I=\(\dfrac{U}{Rtđ}=0,3A\)
=> Công suất tỏa nhiệt trong mạch là P=U.I=12.0,3=3,6W
b) Ta có \(R2=p.\dfrac{l}{S}=15\Omega=>l=\dfrac{15.S}{p}=\dfrac{15.0,06.10^{-6}}{0,5.10^{-6}}=1,8m\)
c) Mạch (R1ntR2)//R3=>RTđ=\(\dfrac{40.x}{40+x}\Omega\) ( Đặt R3=x)
=>Pab=\(\dfrac{U^2}{Rtđ}=\dfrac{144}{\dfrac{40x}{40+x}}=18=>x=R3=10\Omega\)=>I=\(\dfrac{U}{Rtđ}=\dfrac{12}{8}=1,5A\)
Vậy......

MCD: R1ntR2
a, \(R_{tđ}=R_1+R_2=30+10=40\left(\Omega\right)\)
\(I=\dfrac{U}{R_{tđ}}=\dfrac{12}{40}=0,3\left(A\right)\)
b,Đổi 0,2 mm2=2.10-7 m2
\(l=\dfrac{R_2\cdot S}{\rho}=\dfrac{10\cdot2\cdot10^{-7}}{0,4\cdot10^{-6}}=5\left(m\right)\)
c, MCD R1nt(R3//R2)
\(R_{23}=\dfrac{R_2R_3}{R_2+R_3}=\dfrac{10\cdot20}{10+20}=\dfrac{20}{3}\left(\Omega\right)\)
\(R_{tđ}'=R_1+R_{23}=30+\dfrac{20}{3}=\dfrac{110}{3}\left(\Omega\right)\)
\(I_{23}=I_1=I'=\dfrac{U}{R'_{tđ}}=\dfrac{12}{\dfrac{110}{3}}=\dfrac{18}{55}\left(A\right)\)
\(U_2=U_3=U_{23}=R_{23}\cdot I_{23}=\dfrac{20}{3}\cdot\dfrac{18}{55}=\dfrac{24}{11}\left(V\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{\dfrac{24}{11}}{10}=\dfrac{12}{55}\left(A\right);I_3=\dfrac{U_3}{R_3}=\dfrac{\dfrac{24}{11}}{20}=\dfrac{6}{55}\left(A\right)\)

\(a,R_{tđ}=R_1+R_2=12+24=36\Omega\\ b,R_{tđ}'=R_1+\dfrac{R_2.R_3}{R_2+R_3}=12+\dfrac{24.48}{24+48}=28\Omega\\ I=\dfrac{U_{AB}}{R_{tđ}}=\dfrac{36}{28}=\dfrac{9}{7}A\\ Vì.R_1ntR_{23}\Rightarrow I=I_1=I_{23}=\dfrac{9}{7}A\\ U_1=R_1.I_1=12\cdot\dfrac{9}{7}=\dfrac{108}{7}V\\ U_{23}=U_{AB}-U_1=36-\dfrac{108}{7}=\dfrac{144}{7}V\\ Vì.R_2//R_3\Rightarrow U_{23}=U_2=U_3=\dfrac{144}{7}V\\ I_3=\dfrac{U_3}{R_3}=\dfrac{144:7}{48}=\dfrac{3}{7}A\\ P_{3\left(hoa\right)}=U_3.I_3=\dfrac{144}{7}\cdot\dfrac{3}{7}\approx8,82W\)

a) Vì R1 nt R2 nên: Rtd = R1 + R2= 24+12= 36(ôm)
R1 nt R2 thì: I= I1= I2 = 0,5 (A)
HĐT giữa 2 đầu mỗi điện trờ là: I1=U1/R1 => U1=I1.R1 = 0,5 x 24= 12 (V)
I2=U2/R2 => U2=I2.R2= 0,5 x 12= 6(V)
b) Đổi: 20p = 1200s
Nhiệt lượng toả ra trong 20p của đoạn mạch là: Q= I2.Rtd.t= (0,5)2 . 36.1200= 10800(J)
c) Tóm tắt:
R3//R1
I2=3I1
Giải:

\(R1//R2\Rightarrow Rtd=\dfrac{R1R2}{R1+R2}=24\Omega\Rightarrow Im=\dfrac{U}{Rtd}=\dfrac{12}{24}=0,5A\)
\(\Rightarrow R2//\left(R1ntR3\right)\Rightarrow Im=\dfrac{U}{\dfrac{R2\left(R1+R3\right)}{R2+R1+R3}}=0,4A\)
a) Vì \(R_1ntR_2\)
\(\Rightarrow R_{tđ}=R_1+R_2=25+15=40\left(\Omega\right)\)
b) Cường độ dòng điện chạy trong mạch:
\(I_1=I_2=I=\frac{U}{R_{tđ}}=\frac{12}{40}=0,3\left(A\right)\)
Công suất tỏa nhiệt:
\(P=R_{tđ}.I^2=40.0,3^2=12\left(W\right)\)
c) Chiều dài dây dẫn:
\(R=p\frac{l}{S}\Rightarrow l=\frac{R.S}{p}=\frac{15.0,00000006}{0,5.10^{-6}}=0,18\left(m\right)\)
d) Cường độ dòng điện:
\(I=\frac{P}{U}=\frac{18}{12}=1,5\left(A\right)\)
Điện trở tương tương:
\(R_{tđ}'=\frac{U}{I}=\frac{12}{1,5}=8\left(\Omega\right)\)
Điện trở R3:
\(R_{tđ}'=\frac{R_{tđ}.R_3}{R_{tđ}+R_3}\Rightarrow R_3=20\left(\Omega\right)\)
Vậy ...