Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A=|m+1|+|m-1|=|m+1|+|1-m|>=|m+1+1-m|=2
Dấu = xảy ra khi -1<=m<=1
B=|2a-1|+|2a-3|=|2a-1|+|3-2a|>=|2a-1+3-2a|=2
Dấu = xảy ra khi 1/2<=a<=3/2

a) x + \(\sqrt{\left(x-2^{ }\right)^2}\)= x +\(|x-2|\)= x +2-x (vì x<2)
b) \(\sqrt{\left(x-3\right)^2}\)-x = \(|x-3|-x=x-3-x\) (vì x>3)
c) m- \(\sqrt{m^2-2m+1}=m-\sqrt{\left(m-1\right)^2}\)
Những con còn lại bạn làm như trên và rút gọn đi là được
d: \(=x+y-\left|x-y\right|\)
=x+y-x+y=2y
e: \(=\left|5a-1\right|-4a=\left|5\cdot\dfrac{1}{2}-1\right|-2\)
\(=\dfrac{5}{2}-1-2=\dfrac{5}{2}-3=-\dfrac{1}{2}\)
f: \(=\left|2a-3\right|-4a-1\)
\(=\left|-10-3\right|-4\cdot\left(-5\right)-1=13+20-1=32\)

a/ \(\sqrt{4a^4-12a^2+9}-\sqrt{a^4-8a^2+16}\)
= \(\sqrt{\left(2a^2-3\right)^2}-\sqrt{\left(a^2-4\right)^2}\)
= \(|2a^2-3|-|a^2-4|\)
= \(2a^2-3+a^2-4\)
= \(3a^2-7\)
Thay a=\(\sqrt{3}\).Ta có:
\(3.\left(\sqrt{3}\right)^2-7\)
= 3.3-7=2
b/ \(\sqrt{10a^2-12a\sqrt{10}+36}\)
= \(\sqrt{\left(a\sqrt{10}\right)^2-2.a\sqrt{10}.6+6^2}\)
= \(\sqrt{\left(a\sqrt{10}-6\right)^2}\)
= \(|a\sqrt{10}-6|\)
= \(-a\sqrt{10}+6\)
Thay a= \(\sqrt{\frac{5}{2}}-\sqrt{\frac{2}{5}}\)=\(\frac{3}{\sqrt{10}}\),Ta có:
\(-\frac{3}{\sqrt{10}}.\sqrt{10}+6\)
= -3+6 =3

a) \(\sqrt{-9a}-\sqrt{9+12a+4a^2}\) \(=\sqrt{9.\left(-a\right)}-\sqrt{\left(3+2a\right)^2}=3\sqrt{-a}-\left|3+2a\right|\)
\(=3\sqrt{9}-\left|3+2\left(-9\right)\right|=3.3-15=-6\)
b) \(1+\dfrac{3m}{m-2}\sqrt{m^2-4x+4}=1+\dfrac{3m}{m-2}\sqrt{\left(m-2\right)^2}=1+\dfrac{3m\left|m-2\right|}{m-2}\)
\(=\left\{{}\begin{matrix}1+3m\left(nếu\left(m-2\right)>0\right)\\1-3m\left(nến\left(m-2\right)< 0\right)\end{matrix}\right.\) \(=\left\{{}\begin{matrix}1+3m\left(nếu\left(m>2\right)\right)\\1-3m\left(nếu\left(m< 2\right)\right)\end{matrix}\right.\)
ta có : \(m=1,5< 2\) vậy giá trị của biểu thức tại m = 1,5 là \(1-3m\) = \(1-3.1,5=-3,5\)
c) \(\sqrt{1-10a+25a^2}-4a=\sqrt{\left(1-5a\right)^2}-4a=\left|1-5a\right|-4a\)
\(=\left\{{}\begin{matrix}1-9a\left(nếu\left(1-5a\right)\ge0\right)\\a-1\left(nếu\left(1-5a\right)< 0\right)\end{matrix}\right.\) \(=\left\{{}\begin{matrix}1-9a\left(nếu\left(a\le\dfrac{1}{5}\right)\right)\\a-1\left(nếu\left(a>\dfrac{1}{5}\right)\right)\end{matrix}\right.\)
ta có : \(a=\sqrt{2}>\dfrac{1}{5}\) vậy giá trị của biểu thức tại \(a=\sqrt{2}\) là a - 1 = \(\sqrt{2}-1\)
d) \(4x-\sqrt{9x^2+6x+1}=4x-\sqrt{\left(3x+1\right)^2}=4x-\left|3x+1\right|\)
\(=\left\{{}\begin{matrix}x-1\left(nếu\left(x\ge-\dfrac{1}{3}\right)\right)\\7x+1\left(nếu\left(x< -\dfrac{1}{3}\right)\right)\end{matrix}\right.\)
ta có : \(x=-\sqrt{3}< -\dfrac{1}{3}\) vậy giá trị của biểu thức tại \(x=-\sqrt{3}\) là \(7.\left(-\sqrt{3}\right)+1=1-7\sqrt{3}\)

Đặt \(\left\{{}\begin{matrix}\sqrt{4a+1}=x\\\sqrt{4b+1}=y\end{matrix}\right.\) \(\Rightarrow1\le x;y\le3\)
\(\Rightarrow x^2+y^2=4\left(a+b\right)+2=10\)
Do \(1\le x\le3\Rightarrow\left(x-1\right)\left(x-3\right)\le0\Rightarrow x^2-4x+3\le0\)
\(\Rightarrow x^2+3\le4x\Rightarrow x\ge\frac{x^2+3}{4}\)
Tương tự, do \(1\le y\le3\Rightarrow y\ge\frac{y^2+3}{4}\)
\(\Rightarrow P=x+y\ge\frac{x^2+3}{4}+\frac{y^2+3}{4}=\frac{x^2+y^2+6}{4}=\frac{16}{4}=4\)
\(\Rightarrow P_{min}=4\) khi \(\left(x;y\right)=\left(1;3\right);\left(3;1\right)\) hay \(\left(a;b\right)=\left(0;2\right);\left(2;0\right)\)

\(a)\sqrt{-9a}-\sqrt{9+12a+4a^2}\)
\(==\sqrt{3^2.\left(-a\right)}-\sqrt{3^2-2.3.2a+\left(2a\right)^2}\)
\(=3\sqrt{-a}-\sqrt{\left(3+2a\right)^2}\)
\(=3\sqrt{a}-\left|3+2a\right|\)
\(b)1+\frac{3m}{m-2}\sqrt{m^2-4m+4}\)
\(=1+\frac{3m}{m-2}\sqrt{\left(m\right)^2-2.2m+2^2}\)
\(=1+\frac{3m}{m-2}\sqrt{\left(m-2\right)^2}\)
\(=1+\frac{3m}{m-2}|m-2|\)
\(c)4x-\sqrt{9x^2+6x+1}\)
\(=4x-\sqrt{\left(3x\right)^2+2.3x+1}\)
\(=4x-\sqrt{\left(3x+1\right)^2}\)
\(=4x-|3x+1|\)

Ta có :
\(A=\sqrt{\left(2a-3b\right)^2}+2\sqrt{\left(b-c\right)^2}+\sqrt{\left(2c-3a\right)^2}\)
\(A=\left|2a-3b\right|+2\left|b-c\right|+\left|2c-3a\right|\)
\(\ge3b-2a+2\left(c-b\right)+\left(3a-2c\right)=a+b\ge2\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}3b-2a,c-b,3a-2c\ge0\\a=b=1\end{cases}\Leftrightarrow\hept{\begin{cases}a=b=1\\1\le c\le\frac{3}{2}\end{cases}}}\)
Vậy Min A = 2 khi a = b = 1 và c \(\in\)\(\left[1,\frac{3}{2}\right]\)

Ý, B vậy chưa gọn, phải viết thành dị đây mới gọn hẳn, xin nha!
B= 2m-m
Tính các số lẻ tẻ ở ngoài luôn.
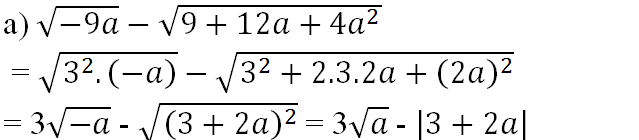
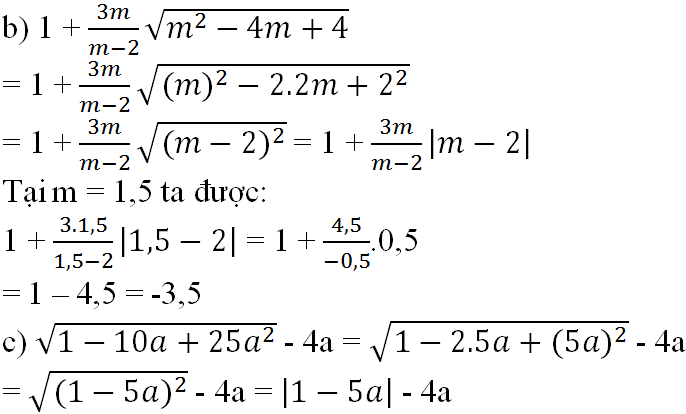

cái phần A là thiếu dấu cộng đấy ạ
Em thử nha!Sai thì thôi:((
\(A=\left|m+1\right|+\left|m-1\right|=\left|m+1\right|+\left|1-m\right|\ge\left|m+1+1-m\right|=2\)
Dấu"=" xảy ra khi \(\left(m+1\right)\left(1-m\right)\ge0\Leftrightarrow-m^2+1\Leftrightarrow-1\le m\le1\)
\(B=\sqrt{\left(2a\right)^2-2.2a.1+1}+\sqrt{4a^2-2.2a.3+9}\)
\(=\left|2a-1\right|+\left|2a-3\right|=\left|2a-1\right|+\left|3-2a\right|\ge2\)
Dấu "=" xảy ra khi...