Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
-21:7/28:4 = -3/4
-39:13/52:13 = -3/4
Vì -3/4 = -3/4 nên -21/28 = -39/52
-1717:101/2323:101 = -17/23
-171717:10101/232323:10101 = -17/23
Vì -17/23 = -17/23 nên -1717/2323 = -171717/232323

Tính các tổng dưới đây sau khi đã rút gọn phân số :
a)\(\dfrac{7}{21}\) + \(\dfrac{9}{-36}\) = \(\dfrac{7}{21}\)+\(\dfrac{-9}{36}\)=\(\dfrac{1}{3}\)+\(\dfrac{-1}{4}\)=\(\dfrac{4}{12}\)+\(\dfrac{-3}{12}\)=\(\dfrac{1}{12}\)
b) \(\dfrac{-12}{18}\)+\(\dfrac{-21}{35}\)=\(\dfrac{-2}{3}\)+\(\dfrac{-3}{5}\)=\(\dfrac{-10}{15}\)+\(\dfrac{-9}{15}\)=\(\dfrac{-19}{15}\)
c) \(\dfrac{-3}{21}\)+\(\dfrac{6}{42}\)=\(\dfrac{-1}{7}\)+\(\dfrac{1}{7}\)=0
d) \(\dfrac{-18}{24}\)+\(\dfrac{15}{-21}\)=\(\dfrac{-18}{24}\)+\(\dfrac{-15}{21}\)=\(\dfrac{-3}{4}\)+\(\dfrac{-5}{7}\)=\(\dfrac{-21}{28}\)+\(\dfrac{-20}{28}\)=\(\dfrac{-41}{28}\)

a)\(\dfrac{-3}{29}+\dfrac{16}{58}\)\(=\dfrac{-3}{29}+\dfrac{8}{29}=\dfrac{5}{29}\)
b) \(\dfrac{8}{40}+\dfrac{-36}{45}=\dfrac{1}{5}+\dfrac{-4}{5}=\dfrac{-3}{5}\)
c) \(\dfrac{-8}{18}+\dfrac{-15}{27}=\dfrac{-4}{9}+\dfrac{-5}{9}=\dfrac{-9}{9}=-1\)
a) \(\dfrac{-3}{29}+\dfrac{16}{58}=\dfrac{-3}{29}+\dfrac{8}{29}=\dfrac{-3+8}{29}=\dfrac{5}{29}\)
b) \(\dfrac{8}{40}+\dfrac{-36}{45}=\dfrac{1}{5}+\dfrac{-4}{5}=\dfrac{1+\left(-4\right)}{5}=\dfrac{-3}{5}\)
c) \(\dfrac{-8}{18}+\dfrac{-15}{27}=\dfrac{-4}{9}+\dfrac{-5}{9}=\dfrac{-4+\left(-5\right)}{9}=\dfrac{-9}{9}=-1\)

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)

a: \(\dfrac{20}{30}=\dfrac{2}{3}\)
\(\dfrac{30}{45}=\dfrac{2}{3}\)
Do đó: \(\dfrac{20}{30}=\dfrac{30}{45}\)
b: \(\dfrac{-25}{35}=\dfrac{-5}{7}\)
\(\dfrac{-55}{77}=\dfrac{-5}{7}\)
Do đó: \(-\dfrac{25}{35}=-\dfrac{55}{77}\)
a,20/30=2/3
30/45=2/3
->20/30=30/45
b -25/35=-5/7
-55/77=-5/7
-> -25/35=-55/77

a: 20/30=2/3
30/45=2/3
=>20/30=30/45
b: -25/35=-5/7
-55/77=-5/7
=>-25/35=-55/77
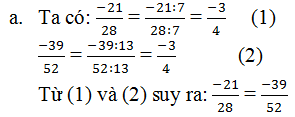

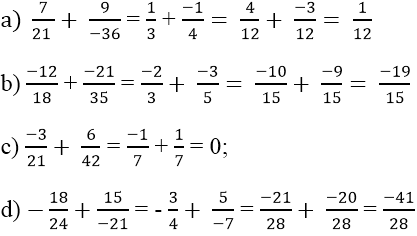


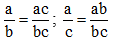
a) Ta có:
\(\dfrac{36}{84}=\dfrac{3}{7}\) ; \(\dfrac{42}{98}=\dfrac{3}{7}\)
\(\Rightarrow\dfrac{36}{84}=\dfrac{42}{98}\left(=\dfrac{3}{7}\right)\)
b) Ta có :
\(\dfrac{123}{237}=\dfrac{41}{79}\) ; \(\dfrac{123123}{237237}=\dfrac{41}{79}\)
\(\Rightarrow\dfrac{123}{237}=\dfrac{123123}{237237}\)
a) Ta rút gọn phân số:
\(\dfrac{36}{84}\)=\(\dfrac{36:12}{84:12}\)=\(\dfrac{3}{7}\)
\(\dfrac{42}{98}\)=\(\dfrac{42:14}{98:14}\)=\(\dfrac{3}{7}\)
Vì \(\dfrac{3}{7}\)=\(\dfrac{3}{7}\) nên \(\dfrac{36}{84}\)=\(\dfrac{42}{98}\)